Data-Driven Estimation of Conditional Expectations, Application to Optimal Stopping and Reinforcement Learning

When the underlying conditional density is known, conditional expectations can be computed analytically or numerically. When, however, such knowledge is not available and instead we are given a collection of training data, the goal of this work is to propose simple and purely data-driven means for estimating directly the desired conditional expectation. Because conditional expectations appear in the description of a number of stochastic optimization problems with the corresponding optimal solution satisfying a system of nonlinear equations, we extend our data-driven method to cover such cases as well. We test our methodology by applying it to Optimal Stopping and Optimal Action Policy in Reinforcement Learning.

Data-Driven Parameter Estimation

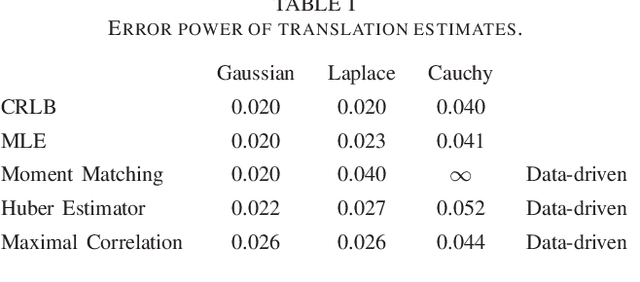
Optimum parameter estimation methods require knowledge of a parametric probability density that statistically describes the available observations. In this work we examine Bayesian and non-Bayesian parameter estimation problems under a data-driven formulation where the necessary parametric probability density is replaced by available data. We present various data-driven versions that either result in neural network approximations of the optimum estimators or in well defined optimization problems that can be solved numerically. In particular, for the data-driven equivalent of non-Bayesian estimation we end up with optimization problems similar to the ones encountered for the design of generative networks.

Image De-Quantization Using Generative Models as Priors

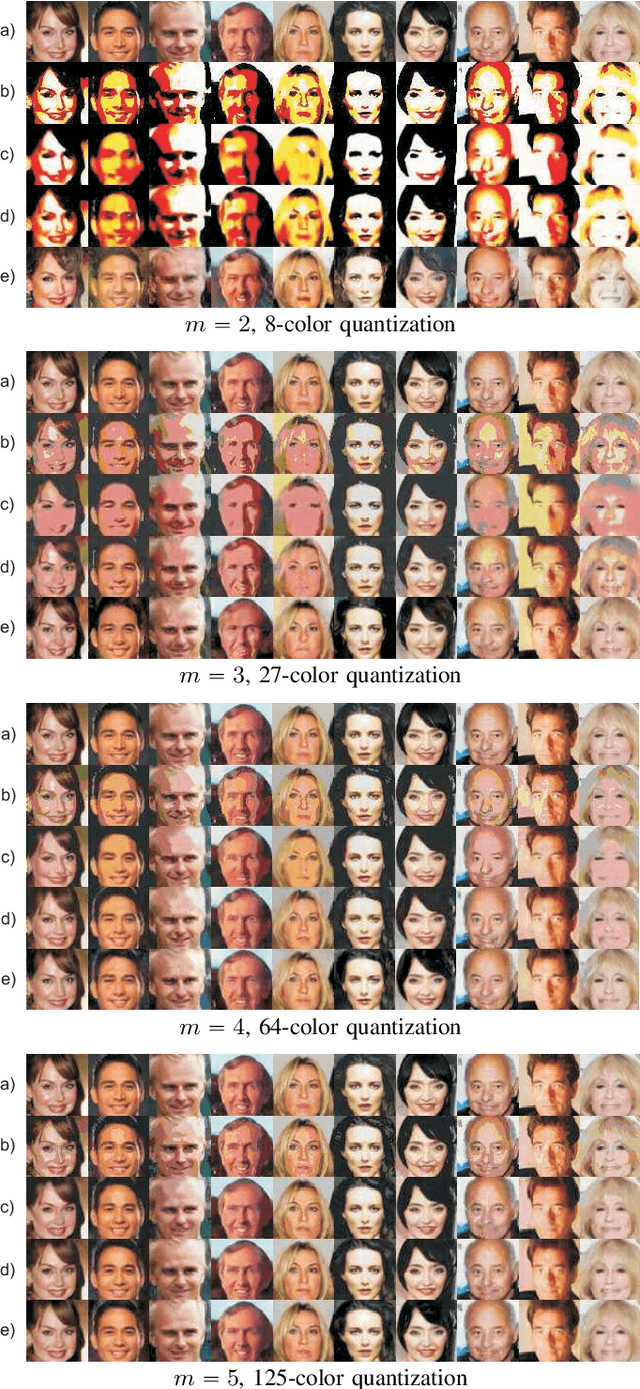
Image quantization is used in several applications aiming in reducing the number of available colors in an image and therefore its size. De-quantization is the task of reversing the quantization effect and recovering the original multi-chromatic level image. Existing techniques achieve de-quantization by imposing suitable constraints on the ideal image in order to make the recovery problem feasible since it is otherwise ill-posed. Our goal in this work is to develop a de-quantization mechanism through a rigorous mathematical analysis which is based on the classical statistical estimation theory. In this effort we incorporate generative modeling of the ideal image as a suitable prior information. The resulting technique is simple and capable of de-quantizing successfully images that have experienced severe quantization effects. Interestingly, our method can recover images even if the quantization process is not exactly known and contains unknown parameters.

Image Restoration from Parametric Transformations using Generative Models

When images are statistically described by a generative model we can use this information to develop optimum techniques for various image restoration problems as inpainting, super-resolution, image coloring, generative model inversion, etc. With the help of the generative model it is possible to formulate, in a natural way, these restoration problems as Statistical estimation problems. Our approach, by combining maximum a-posteriori probability with maximum likelihood estimation, is capable of restoring images that are distorted by transformations even when the latter contain unknown parameters. The resulting optimization is completely defined with no parameters requiring tuning. This must be compared with the current state of the art which requires exact knowledge of the transformations and contains regularizer terms with weights that must be properly defined. Finally, we must mention that we extend our method to accommodate mixtures of multiple images where each image is described by its own generative model and we are able of successfully separating each participating image from a single mixture.

Designing GANs: A Likelihood Ratio Approach

We are interested in the design of generative adversarial networks. The training of these mathematical structures requires the definition of proper min-max optimization problems. We propose a simple methodology for constructing such problems assuring, at the same time, that they provide the correct answer. We give characteristic examples developed by our method, some of which can be recognized from other applications and some introduced for the first time. We compare various possibilities by applying them to well known datasets using neural networks of different configurations and sizes.

Training Neural Networks for Likelihood/Density Ratio Estimation

Various problems in Engineering and Statistics require the computation of the likelihood ratio function of two probability densities. In classical approaches the two densities are assumed known or to belong to some known parametric family. In a data-driven version we replace this requirement with the availability of data sampled from the densities of interest. For most well known problems in Detection and Hypothesis testing we develop solutions by providing neural network based estimates of the likelihood ratio or its transformations. This task necessitates the definition of proper optimizations which can be used for the training of the network. The main purpose of this work is to offer a simple and unified methodology for defining such optimization problems with guarantees that the solution is indeed the desired function. Our results are extended to cover estimates for likelihood ratios of conditional densities and estimates for statistics encountered in local approaches.

Optimizing Shallow Networks for Binary Classification

Data driven classification that relies on neural networks is based on optimization criteria that involve some form of distance between the output of the network and the desired label. Using the same mathematical mathematical analysis, for a multitude of such measures, we can show that their optimum solution matches the ideal likelihood ratio test classifier. In this work we introduce a different family of optimization problems which is not covered by the existing approaches and, therefore, opens possibilities for new training algorithms for neural network based classification. We give examples that lead to algorithms that are simple in implementation, exhibit stable convergence characteristics and are antagonistic to the most popular existing techniques.

Kernel-Based Training of Generative Networks

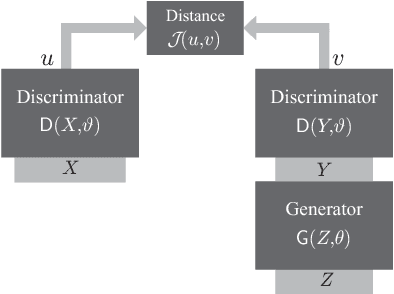
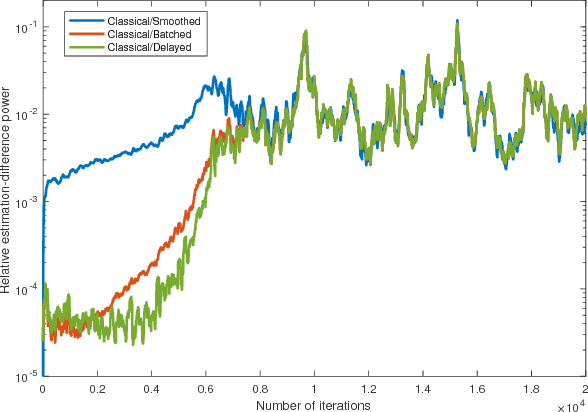
Generative adversarial networks (GANs) are designed with the help of min-max optimization problems that are solved with stochastic gradient-type algorithms which are known to be non-robust. In this work we revisit a non-adversarial method based on kernels which relies on a pure minimization problem and propose a simple stochastic gradient algorithm for the computation of its solution. Using simplified tools from Stochastic Approximation theory we demonstrate that batch versions of the algorithm or smoothing of the gradient do not improve convergence. These observations allow for the development of a training algorithm that enjoys reduced computational complexity and increased robustness while exhibiting similar synthesis characteristics as classical GANs.

Sampling-based Roadmap Planners are Probably Near-Optimal after Finite Computation

Sampling-based motion planners have proven to be efficient solutions to a variety of high-dimensional, geometrically complex motion planning problems with applications in several domains. The traditional view of these approaches is that they solve challenges efficiently by giving up formal guarantees and instead attain asymptotic properties in terms of completeness and optimality. Recent work has argued based on Monte Carlo experiments that these approaches also exhibit desirable probabilistic properties in terms of completeness and optimality after finite computation. The current paper formalizes these guarantees. It proves a formal bound on the probability that solutions returned by asymptotically optimal roadmap-based methods (e.g., PRM*) are within a bound of the optimal path length I* with clearance {\epsilon} after a finite iteration n. This bound has the form P(|In - I* | {\leq} {\delta}I*) {\leq} Psuccess, where {\delta} is an error term for the length a path in the PRM* graph, In. This bound is proven for general dimension Euclidean spaces and evaluated in simulation. A discussion on how this bound can be used in practice, as well as bounds for sparse roadmaps are also provided.