Manipulating Deformable Objects by Interleaving Prediction, Planning, and Control

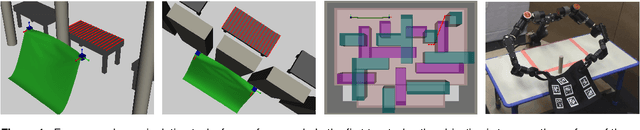
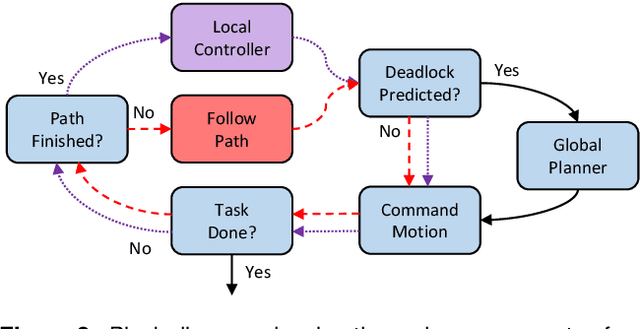
We present a framework for deformable object manipulation that interleaves planning and control, enabling complex manipulation tasks without relying on high-fidelity modeling or simulation. The key question we address is when should we use planning and when should we use control to achieve the task? Planners are designed to find paths through complex configuration spaces, but for highly underactuated systems, such as deformable objects, achieving a specific configuration is very difficult even with high-fidelity models. Conversely, controllers can be designed to achieve specific configurations, but they can be trapped in undesirable local minima due to obstacles. Our approach consists of three components: (1) A global motion planner to generate gross motion of the deformable object; (2) A local controller for refinement of the configuration of the deformable object; and (3) A novel deadlock prediction algorithm to determine when to use planning versus control. By separating planning from control we are able to use different representations of the deformable object, reducing overall complexity and enabling efficient computation of motion. We provide a detailed proof of probabilistic completeness for our planner, which is valid despite the fact that our system is underactuated and we do not have a steering function. We then demonstrate that our framework is able to successfully perform several manipulation tasks with rope and cloth in simulation which cannot be performed using either our controller or planner alone. These experiments suggest that our planner can generate paths efficiently, taking under a second on average to find a feasible path in three out of four scenarios. We also show that our framework is effective on a 16 DoF physical robot, where reachability and dual-arm constraints make the planning more difficult.

dRRT*: Scalable and Informed Asymptotically-Optimal Multi-Robot Motion Planning

Many exciting robotic applications require multiple robots with many degrees of freedom, such as manipulators, to coordinate their motion in a shared workspace. Discovering high-quality paths in such scenarios can be achieved, in principle, by exploring the composite space of all robots. Sampling-based planners do so by building a roadmap or a tree data structure in the corresponding configuration space and can achieve asymptotic optimality. The hardness of motion planning, however, renders the explicit construction of such structures in the composite space of multiple robots impractical. This work proposes a scalable solution for such coupled multi-robot problems, which provides desirable path-quality guarantees and is also computationally efficient. In particular, the proposed \drrtstar\ is an informed, asymptotically-optimal extension of a prior sampling-based multi-robot motion planner, \drrt. The prior approach introduced the idea of building roadmaps for each robot and implicitly searching the tensor product of these structures in the composite space. This work identifies the conditions for convergence to optimal paths in multi-robot problems, which the prior method was not achieving. Building on this analysis, \drrt\ is first properly adapted so as to achieve the theoretical guarantees and then further extended so as to make use of effective heuristics when searching the composite space of all robots. The case where the various robots share some degrees of freedom is also studied. Evaluation in simulation indicates that the new algorithm, \drrtstar\, converges to high-quality paths quickly and scales to a higher number of robots where various alternatives fail. This work also demonstrates the planner's capability to solve problems involving multiple real-world robotic arms.

Scalable Asymptotically-Optimal Multi-Robot Motion Planning

Finding asymptotically-optimal paths in multi-robot motion planning problems could be achieved, in principle, using sampling-based planners in the composite configuration space of all of the robots in the space. The dimensionality of this space increases with the number of robots, rendering this approach impractical. This work focuses on a scalable sampling-based planner for coupled multi-robot problems that provides asymptotic optimality. It extends the dRRT approach, which proposed building roadmaps for each robot and searching an implicit roadmap in the composite configuration space. This work presents a new method, dRRT* , and develops theory for scalable convergence to optimal paths in multi-robot problems. Simulated experiments indicate dRRT* converges to high-quality paths while scaling to higher numbers of robots where the naive approach fails. Furthermore, dRRT* is applicable to high-dimensional problems, such as planning for robot manipulators

Similar Part Rearrangement With Pebble Graphs

This work proposes a method for effectively computing manipulation paths to rearrange similar objects in a cluttered space. The solution can be used to place similar products in a factory floor in a desirable arrangement or for retrieving a particular object from a shelf blocked by similarly sized objects. These are challenging problems as they involve combinatorially large, continuous configuration spaces due to the presence of multiple moving bodies and kinematically complex manipulators. This work leverages ideas from algorithmic theory, multi-robot motion planning and manipulation planning to propose appropriate graphical representations for this challenge. These representations allow to quickly reason whether manipulation paths allow the transition between entire sets of objects arrangements without having to explicitly enumerate the path for each pair of arrangements. The proposed method also allows to take advantage of precomputation given a manipulation roadmap for transferring a single object in the same cluttered space. The resulting approach is evaluated in simulation for a realistic model of a Baxter robot and executed in open-loop on the real system, showing that the approach solves complex instances and is promising in terms of scalability and success ratio.

Sampling-based Roadmap Planners are Probably Near-Optimal after Finite Computation

Sampling-based motion planners have proven to be efficient solutions to a variety of high-dimensional, geometrically complex motion planning problems with applications in several domains. The traditional view of these approaches is that they solve challenges efficiently by giving up formal guarantees and instead attain asymptotic properties in terms of completeness and optimality. Recent work has argued based on Monte Carlo experiments that these approaches also exhibit desirable probabilistic properties in terms of completeness and optimality after finite computation. The current paper formalizes these guarantees. It proves a formal bound on the probability that solutions returned by asymptotically optimal roadmap-based methods (e.g., PRM*) are within a bound of the optimal path length I* with clearance {\epsilon} after a finite iteration n. This bound has the form P(|In - I* | {\leq} {\delta}I*) {\leq} Psuccess, where {\delta} is an error term for the length a path in the PRM* graph, In. This bound is proven for general dimension Euclidean spaces and evaluated in simulation. A discussion on how this bound can be used in practice, as well as bounds for sparse roadmaps are also provided.