Kernel-Based Training of Generative Networks

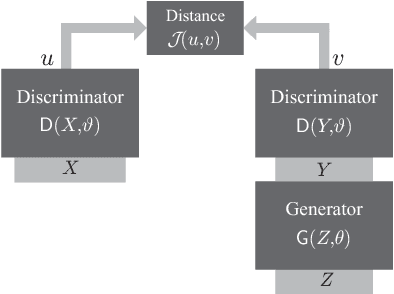
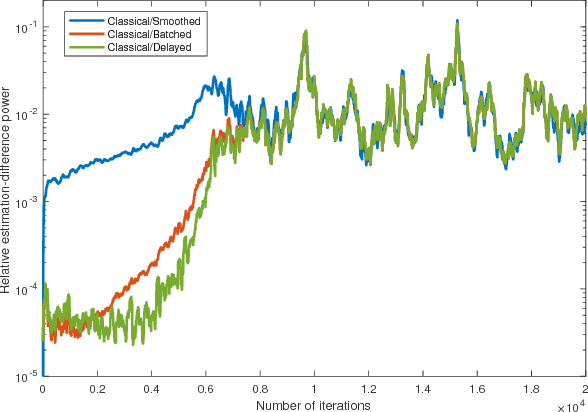
Generative adversarial networks (GANs) are designed with the help of min-max optimization problems that are solved with stochastic gradient-type algorithms which are known to be non-robust. In this work we revisit a non-adversarial method based on kernels which relies on a pure minimization problem and propose a simple stochastic gradient algorithm for the computation of its solution. Using simplified tools from Stochastic Approximation theory we demonstrate that batch versions of the algorithm or smoothing of the gradient do not improve convergence. These observations allow for the development of a training algorithm that enjoys reduced computational complexity and increased robustness while exhibiting similar synthesis characteristics as classical GANs.