Baking Symmetry into GFlowNets

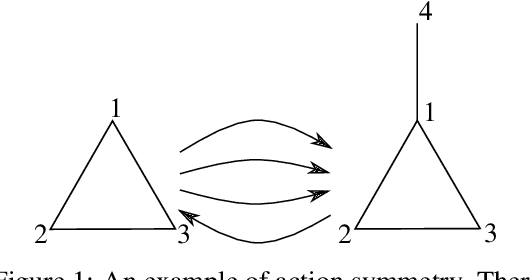
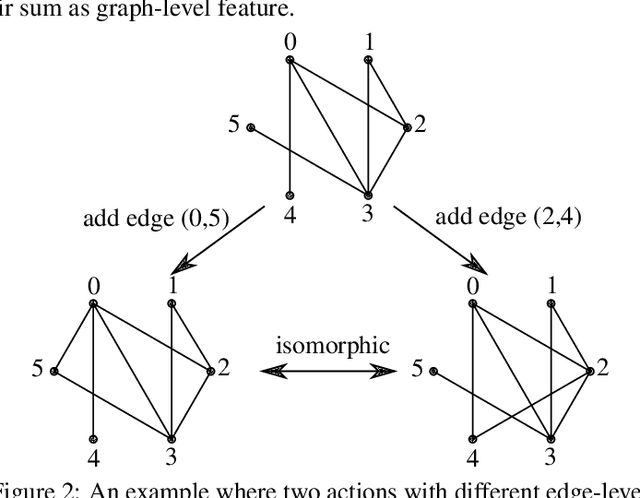
GFlowNets have exhibited promising performance in generating diverse candidates with high rewards. These networks generate objects incrementally and aim to learn a policy that assigns probability of sampling objects in proportion to rewards. However, the current training pipelines of GFlowNets do not consider the presence of isomorphic actions, which are actions resulting in symmetric or isomorphic states. This lack of symmetry increases the amount of samples required for training GFlowNets and can result in inefficient and potentially incorrect flow functions. As a consequence, the reward and diversity of the generated objects decrease. In this study, our objective is to integrate symmetries into GFlowNets by identifying equivalent actions during the generation process. Experimental results using synthetic data demonstrate the promising performance of our proposed approaches.

A Canonization Perspective on Invariant and Equivariant Learning

In many applications, we desire neural networks to exhibit invariance or equivariance to certain groups due to symmetries inherent in the data. Recently, frame-averaging methods emerged to be a unified framework for attaining symmetries efficiently by averaging over input-dependent subsets of the group, i.e., frames. What we currently lack is a principled understanding of the design of frames. In this work, we introduce a canonization perspective that provides an essential and complete view of the design of frames. Canonization is a classic approach for attaining invariance by mapping inputs to their canonical forms. We show that there exists an inherent connection between frames and canonical forms. Leveraging this connection, we can efficiently compare the complexity of frames as well as determine the optimality of certain frames. Guided by this principle, we design novel frames for eigenvectors that are strictly superior to existing methods -- some are even optimal -- both theoretically and empirically. The reduction to the canonization perspective further uncovers equivalences between previous methods. These observations suggest that canonization provides a fundamental understanding of existing frame-averaging methods and unifies existing equivariant and invariant learning methods.