Multiple Instance Verification

We explore multiple-instance verification, a problem setting where a query instance is verified against a bag of target instances with heterogeneous, unknown relevancy. We show that naive adaptations of attention-based multiple instance learning (MIL) methods and standard verification methods like Siamese neural networks are unsuitable for this setting: directly combining state-of-the-art (SOTA) MIL methods and Siamese networks is shown to be no better, and sometimes significantly worse, than a simple baseline model. Postulating that this may be caused by the failure of the representation of the target bag to incorporate the query instance, we introduce a new pooling approach named ``cross-attention pooling'' (CAP). Under the CAP framework, we propose two novel attention functions to address the challenge of distinguishing between highly similar instances in a target bag. Through empirical studies on three different verification tasks, we demonstrate that CAP outperforms adaptations of SOTA MIL methods and the baseline by substantial margins, in terms of both classification accuracy and quality of the explanations provided for the classifications. Ablation studies confirm the superior ability of the new attention functions to identify key instances.

Cross-domain Few-shot Meta-learning Using Stacking

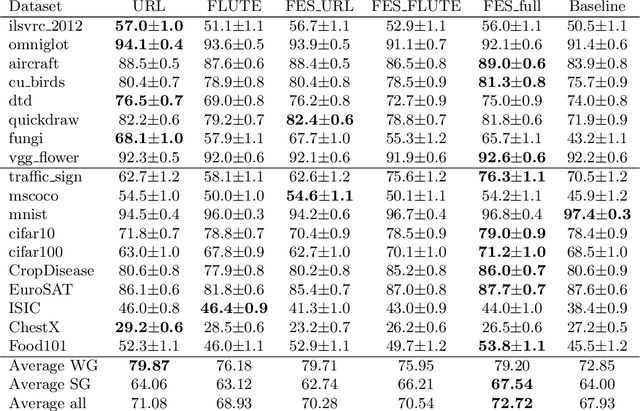
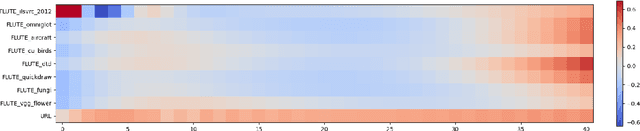
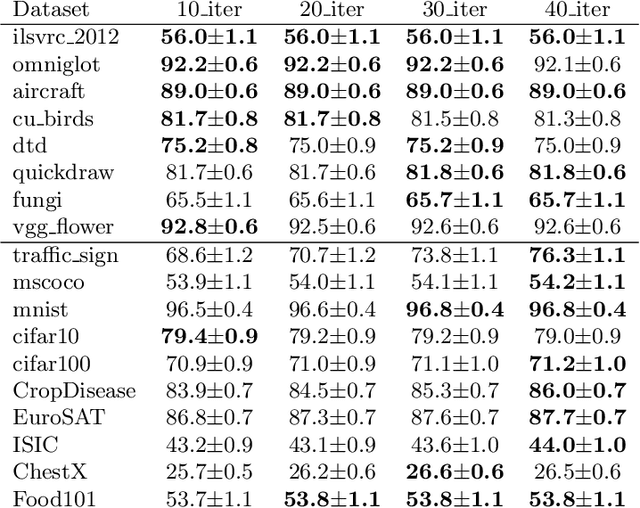
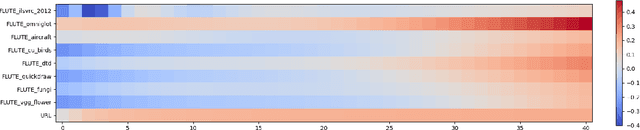
Cross-domain few-shot meta-learning (CDFSML) addresses learning problems where knowledge needs to be transferred from several source domains into an instance-scarce target domain with an explicitly different input distribution. Recently published CDFSML methods generally construct a "universal model" that combines knowledge of multiple source domains into one backbone feature extractor. This enables efficient inference but necessitates re-computation of the backbone whenever a new source domain is added. Moreover, state-of-the-art methods derive their universal model from a collection of backbones -- normally one for each source domain -- and the backbones may be constrained to have the same architecture as the universal model. We propose a CDFSML method that is inspired by the classic stacking approach to meta learning. It imposes no constraints on the backbones' architecture or feature shape and does not incur the computational overhead of (re-)computing a universal model. Given a target-domain task, it fine-tunes each backbone independently, uses cross-validation to extract meta training data from the task's instance-scarce support set, and learns a simple linear meta classifier from this data. We evaluate our stacking approach on the well-known Meta-Dataset benchmark, targeting image classification with convolutional neural networks, and show that it often yields substantially higher accuracy than competing methods.

Sampling Permutations for Shapley Value Estimation

Game-theoretic attribution techniques based on Shapley values are used extensively to interpret black-box machine learning models, but their exact calculation is generally NP-hard, requiring approximation methods for non-trivial models. As the computation of Shapley values can be expressed as a summation over a set of permutations, a common approach is to sample a subset of these permutations for approximation. Unfortunately, standard Monte Carlo sampling methods can exhibit slow convergence, and more sophisticated quasi Monte Carlo methods are not well defined on the space of permutations. To address this, we investigate new approaches based on two classes of approximation methods and compare them empirically. First, we demonstrate quadrature techniques in a RKHS containing functions of permutations, using the Mallows kernel to obtain explicit convergence rates of $O(1/n)$, improving on $O(1/\sqrt{n})$ for plain Monte Carlo. The RKHS perspective also leads to quasi Monte Carlo type error bounds, with a tractable discrepancy measure defined on permutations. Second, we exploit connections between the hypersphere $\mathbb{S}^{d-2}$ and permutations to create practical algorithms for generating permutation samples with good properties. Experiments show the above techniques provide significant improvements for Shapley value estimates over existing methods, converging to a smaller RMSE in the same number of model evaluations.

GPUTreeShap: Fast Parallel Tree Interpretability

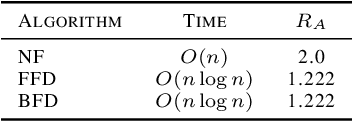
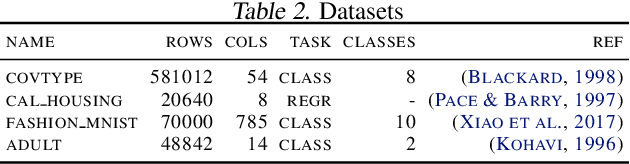
SHAP (SHapley Additive exPlanation) values provide a game theoretic interpretation of the predictions of machine learning models based on Shapley values. While SHAP values are intractable in general, a recursive polynomial time algorithm specialised for decision tree models is available, named TreeShap. Despite its polynomial time complexity, TreeShap can become a significant bottleneck in practical machine learning pipelines when applied to large decision tree ensembles. We present GPUTreeShap, a software package implementing a modified TreeShap algorithm in CUDA for Nvidia GPUs. Our approach first preprocesses the input model to isolate variable sized sub-problems from the original recursive algorithm, then solves a bin packing problem, and finally maps sub-problems to streaming multiprocessors for parallel execution with specialised hardware instructions. With a single GPU, we achieve speedups of up to 19x for SHAP values, and 340x for SHAP interaction values, over a state-of-the-art multi-core CPU implementation. We also experiment with an 8 GPU DGX-1 system, demonstrating throughput of 1.2M rows per second---equivalent CPU-based performance is estimated to require 6850 CPU cores.

On the Calibration of Nested Dichotomies for Large Multiclass Tasks

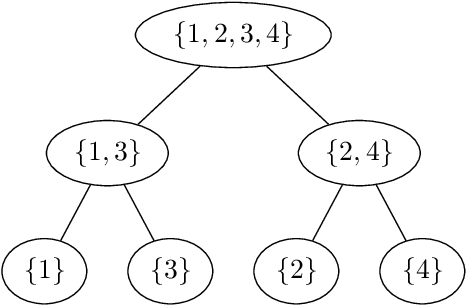
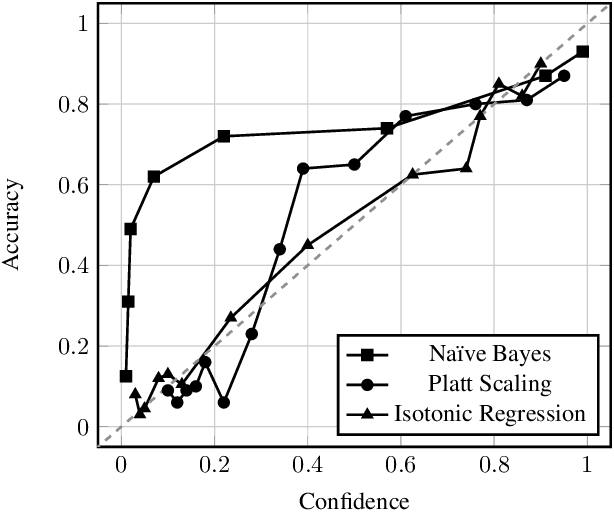
Nested dichotomies are used as a method of transforming a multiclass classification problem into a series of binary problems. A tree structure is induced that recursively splits the set of classes into subsets, and a binary classification model learns to discriminate between the two subsets of classes at each node. In this paper, we demonstrate that these nested dichotomies typically exhibit poor probability calibration, even when the base binary models are well calibrated. We also show that this problem is exacerbated when the binary models are poorly calibrated. We discuss the effectiveness of different calibration strategies and show that accuracy and log-loss can be significantly improved by calibrating both the internal base models and the full nested dichotomy structure, especially when the number of classes is high.

Probability Calibration Trees

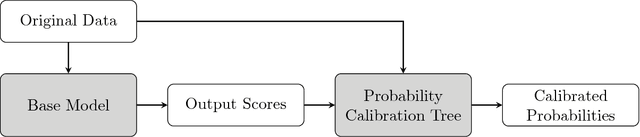
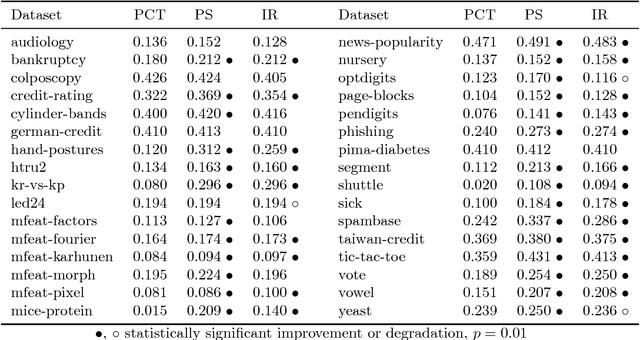
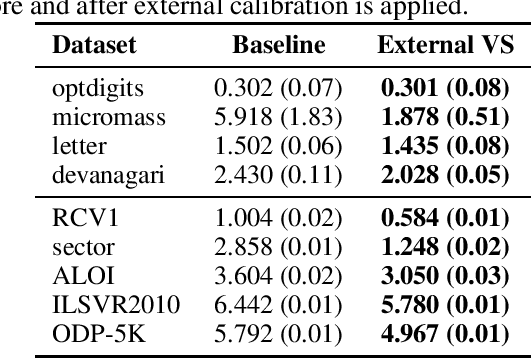
Obtaining accurate and well calibrated probability estimates from classifiers is useful in many applications, for example, when minimising the expected cost of classifications. Existing methods of calibrating probability estimates are applied globally, ignoring the potential for improvements by applying a more fine-grained model. We propose probability calibration trees, a modification of logistic model trees that identifies regions of the input space in which different probability calibration models are learned to improve performance. We compare probability calibration trees to two widely used calibration methods---isotonic regression and Platt scaling---and show that our method results in lower root mean squared error on average than both methods, for estimates produced by a variety of base learners.

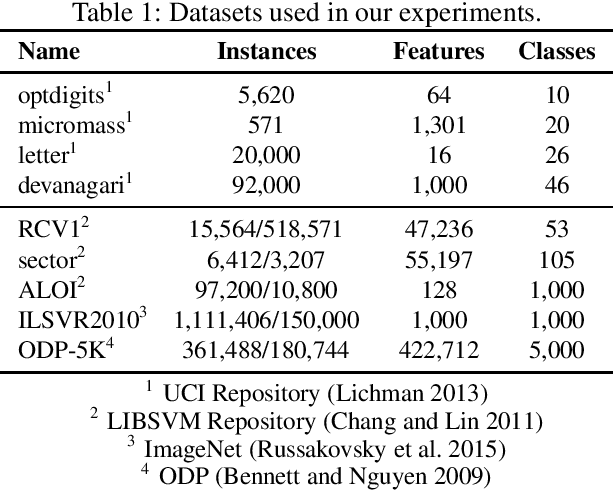
Ensembles of Nested Dichotomies with Multiple Subset Evaluation

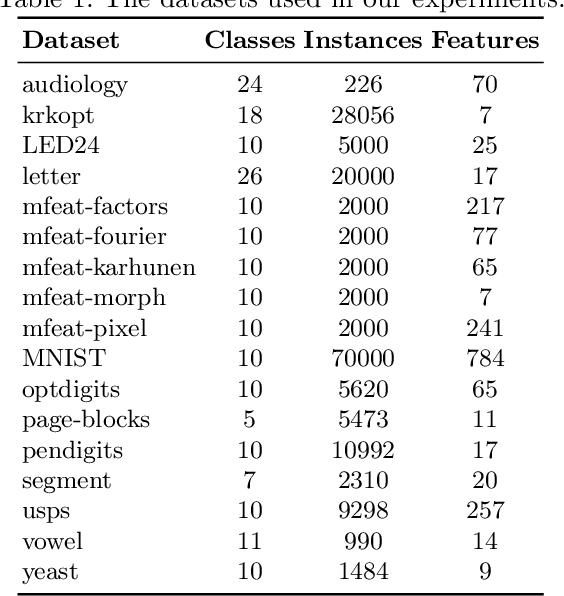
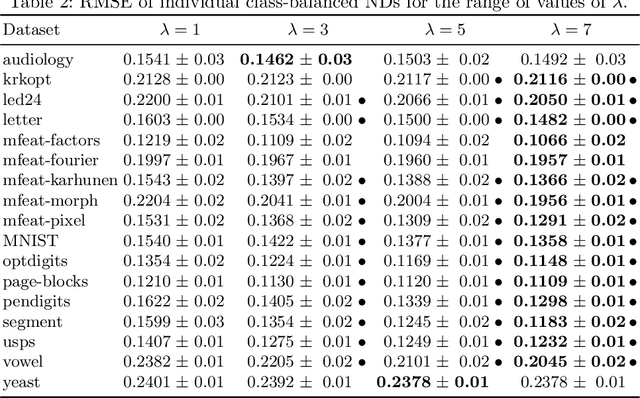
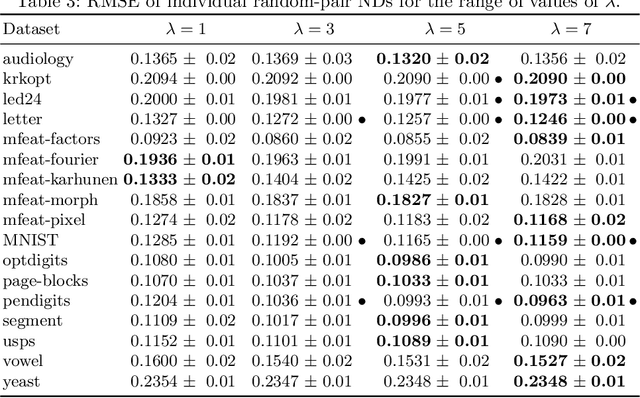
A system of nested dichotomies is a method of decomposing a multi-class problem into a collection of binary problems. Such a system recursively applies binary splits to divide the set of classes into two subsets, and trains a binary classifier for each split. Many methods have been proposed to perform this split, each with various advantages and disadvantages. In this paper, we present a simple, general method for improving the predictive performance of nested dichotomies produced by any subset selection techniques that employ randomness to construct the subsets. We provide a theoretical expectation for performance improvements, as well as empirical results showing that our method improves the root mean squared error of nested dichotomies, regardless of whether they are employed as an individual model or in an ensemble setting.