Temporal Probability Calibration

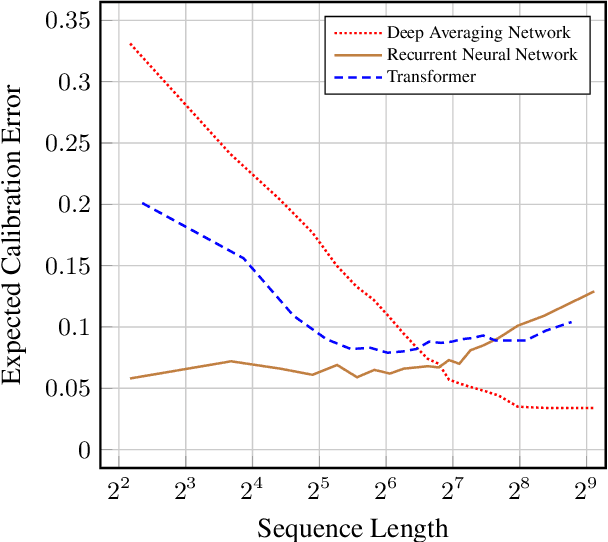
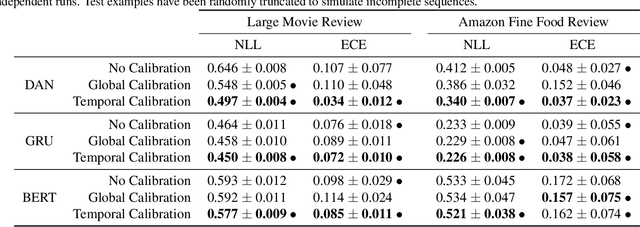
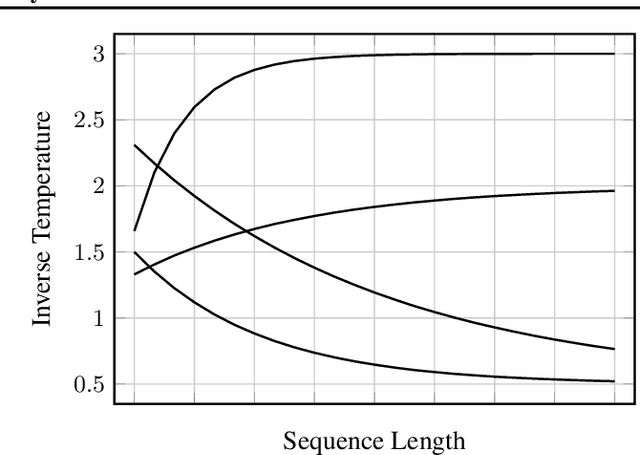
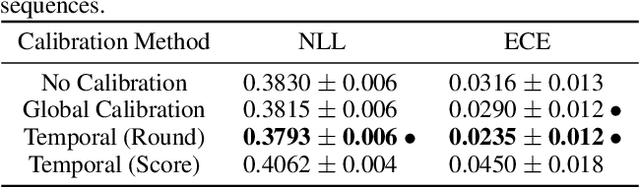
In many applications, accurate class probability estimates are required, but many types of models produce poor quality probability estimates despite achieving acceptable classification accuracy. Even though probability calibration has been a hot topic of research in recent times, the majority of this has investigated non-sequential data. In this paper, we consider calibrating models that produce class probability estimates from sequences of data, focusing on the case where predictions are obtained from incomplete sequences. We show that traditional calibration techniques are not sufficiently expressive for this task, and propose methods that adapt calibration schemes depending on the length of an input sequence. Experimental evaluation shows that the proposed methods are often substantially more effective at calibrating probability estimates from modern sequential architectures for incomplete sequences across a range of application domains.

On the Calibration of Nested Dichotomies for Large Multiclass Tasks

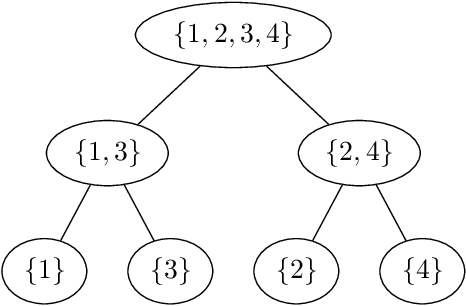
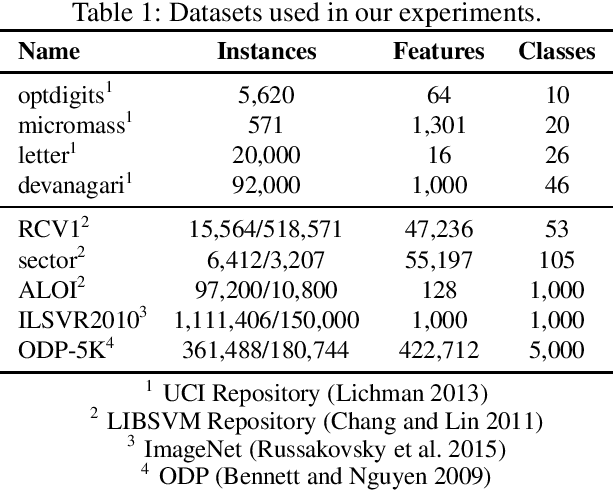
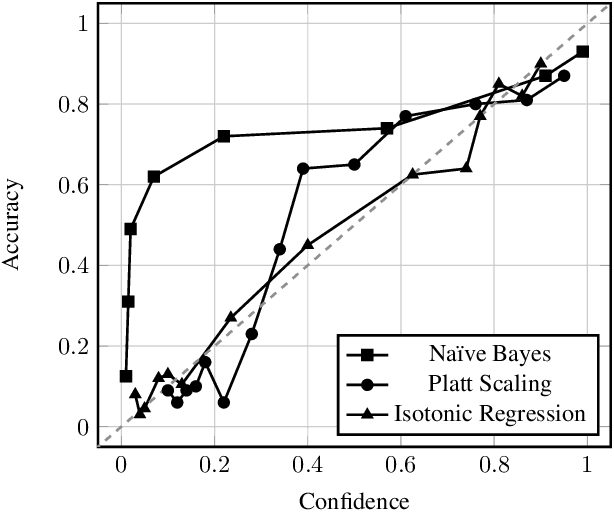
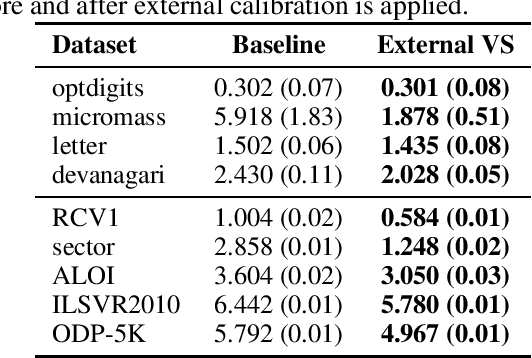
Nested dichotomies are used as a method of transforming a multiclass classification problem into a series of binary problems. A tree structure is induced that recursively splits the set of classes into subsets, and a binary classification model learns to discriminate between the two subsets of classes at each node. In this paper, we demonstrate that these nested dichotomies typically exhibit poor probability calibration, even when the base binary models are well calibrated. We also show that this problem is exacerbated when the binary models are poorly calibrated. We discuss the effectiveness of different calibration strategies and show that accuracy and log-loss can be significantly improved by calibrating both the internal base models and the full nested dichotomy structure, especially when the number of classes is high.

Probability Calibration Trees

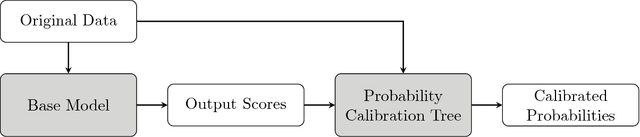
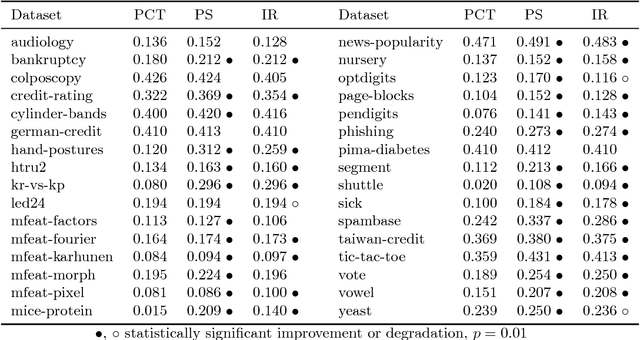
Obtaining accurate and well calibrated probability estimates from classifiers is useful in many applications, for example, when minimising the expected cost of classifications. Existing methods of calibrating probability estimates are applied globally, ignoring the potential for improvements by applying a more fine-grained model. We propose probability calibration trees, a modification of logistic model trees that identifies regions of the input space in which different probability calibration models are learned to improve performance. We compare probability calibration trees to two widely used calibration methods---isotonic regression and Platt scaling---and show that our method results in lower root mean squared error on average than both methods, for estimates produced by a variety of base learners.

Ensembles of Nested Dichotomies with Multiple Subset Evaluation

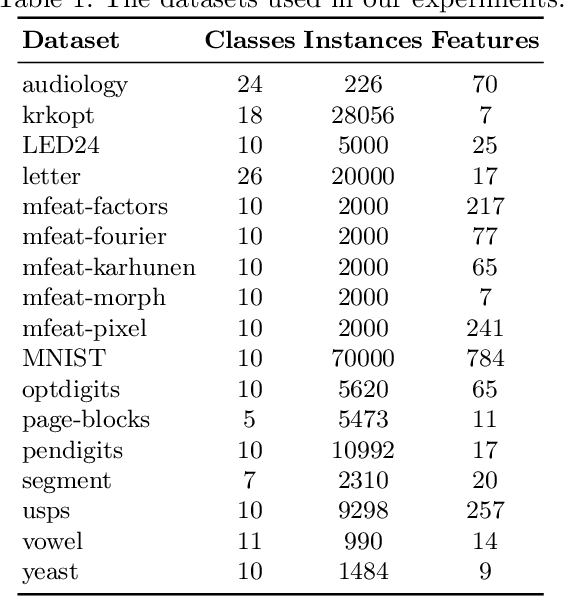
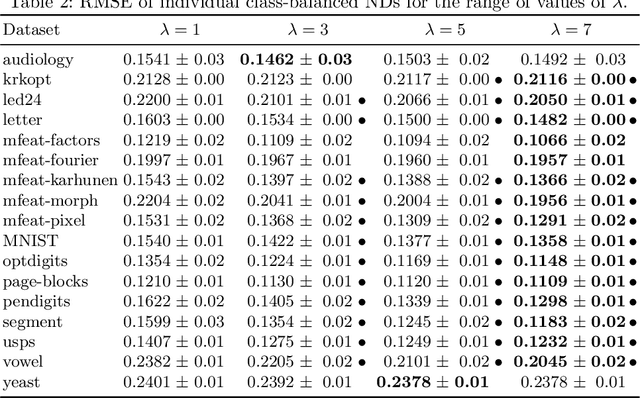
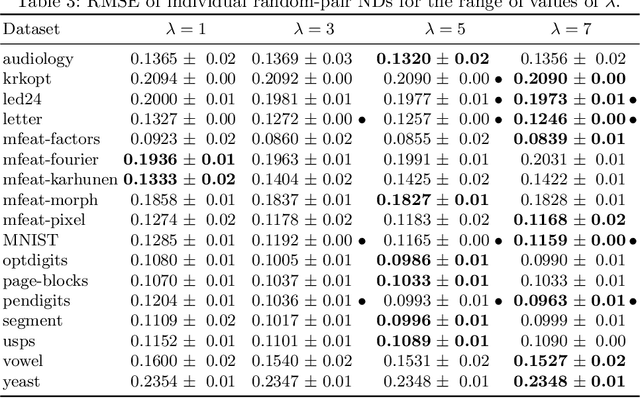
A system of nested dichotomies is a method of decomposing a multi-class problem into a collection of binary problems. Such a system recursively applies binary splits to divide the set of classes into two subsets, and trains a binary classifier for each split. Many methods have been proposed to perform this split, each with various advantages and disadvantages. In this paper, we present a simple, general method for improving the predictive performance of nested dichotomies produced by any subset selection techniques that employ randomness to construct the subsets. We provide a theoretical expectation for performance improvements, as well as empirical results showing that our method improves the root mean squared error of nested dichotomies, regardless of whether they are employed as an individual model or in an ensemble setting.

Building Ensembles of Adaptive Nested Dichotomies with Random-Pair Selection

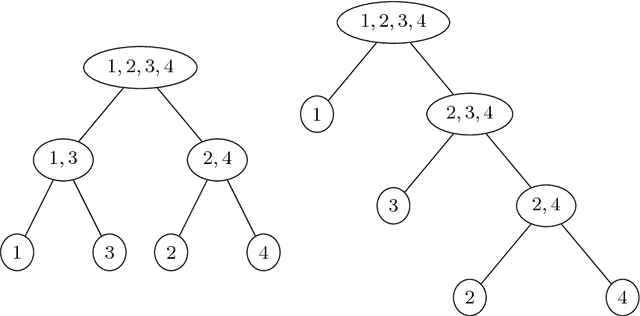
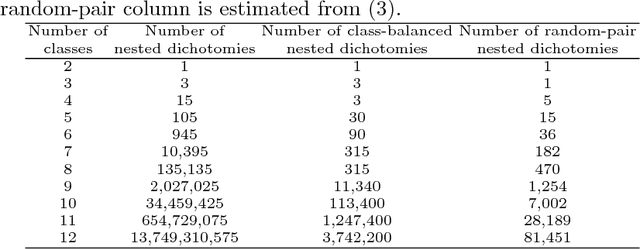
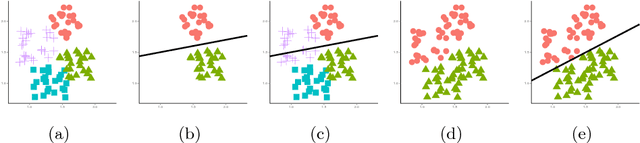
A system of nested dichotomies is a method of decomposing a multi-class problem into a collection of binary problems. Such a system recursively splits the set of classes into two subsets, and trains a binary classifier to distinguish between each subset. Even though ensembles of nested dichotomies with random structure have been shown to perform well in practice, using a more sophisticated class subset selection method can be used to improve classification accuracy. We investigate an approach to this problem called random-pair selection, and evaluate its effectiveness compared to other published methods of subset selection. We show that our method outperforms other methods in many cases when forming ensembles of nested dichotomies, and is at least on par in all other cases.