An Energy-efficient Ordered Transmission-based Sequential Estimation

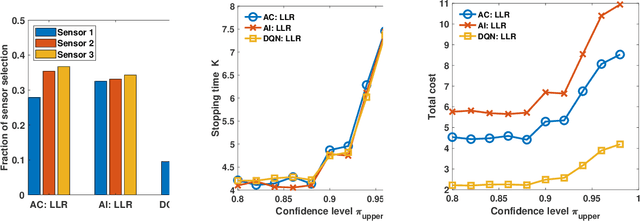
Estimation problems in wireless sensor networks typically involve gathering and processing data from distributed sensors to infer the state of an environment at the fusion center. However, not all measurements contribute significantly to improving estimation accuracy. The ordered transmission protocol, a promising approach for enhancing energy efficiency in wireless networks, allows for the selection of measurements from different sensors to ensure the desired estimation quality. In this work, we use the idea of ordered transmission to reduce the number of transmissions required for sequential estimation within a network, thereby achieving energy-efficient estimation. We derive a new stopping rule that minimizes the number of transmissions while maintaining estimation accuracy similar to general sequential estimation with unordered transmissions. Moreover, we derive the expected number of transmissions required for both general sequential estimation with unordered transmissions and proposed sequential estimation with ordered transmissions and make a comparison between the two systems. Simulation results indicate that our proposed scheme can efficiently reduce transmissions while still ensuring the quality of estimation.

One-bit Compressed Sensing using Generative Models

This paper addresses the classical problem of one-bit compressed sensing using a deep learning-based reconstruction algorithm that leverages a trained generative model to enhance the signal reconstruction performance. The generator, a pre-trained neural network, learns to map from a low-dimensional latent space to a higher-dimensional set of sparse vectors. This generator is then used to reconstruct sparse vectors from their one-bit measurements by searching over its range. The presented algorithm provides an excellent reconstruction performance because the generative model can learn additional structural information about the signal beyond sparsity. Furthermore, we provide theoretical guarantees on the reconstruction accuracy and sample complexity of the algorithm. Through numerical experiments using three publicly available image datasets, MNIST, Fashion-MNIST, and Omniglot, we demonstrate the superior performance of the algorithm compared to other existing algorithms and show that our algorithm can recover both the amplitude and the direction of the signal from one-bit measurements.

Efficient Off-Grid Bayesian Parameter Estimation for Kronecker-Structured Signals

This work studies the problem of jointly estimating unknown parameters from Kronecker-structured multidimensional signals, which arises in applications like intelligent reflecting surface (IRS)-aided channel estimation. Exploiting the Kronecker structure, we decompose the estimation problem into smaller, independent subproblems across each dimension. Each subproblem is posed as a sparse recovery problem using basis expansion and solved using a novel off-grid sparse Bayesian learning (SBL)-based algorithm. Additionally, we derive probabilistic error bounds for the decomposition, quantify its denoising effect, and provide convergence analysis for off-grid SBL. Our simulations show that applying the algorithm to IRS-aided channel estimation improves accuracy and runtime compared to state-of-the-art methods through the low-complexity and denoising benefits of the decomposition step and the high-resolution estimation capabilities of off-grid SBL.

On the Restricted Isometry Property of Kronecker-structured Matrices

In this work, we study the restricted isometry property (RIP) of Kronecker-structured matrices, formed by the Kronecker product of two factor matrices. Previously, only upper and lower bounds on the restricted isometry constant (RIC) in terms of the RICs of the factor matrices were known. We derive a probabilistic measurement bound for the $s$th-order RIC. We show that the Kronecker product of two sub-Gaussian matrices satisfies RIP with high probability if the minimum number of rows among two matrices is $\mathcal{O}(s \ln \max\{N_1, N_2\})$. Here, $s$ is the sparsity level, and $N_1$ and $N_2$ are the number of columns in the matrices. We also present improved measurement bounds for the recovery of Kronecker-structured sparse vectors using Kronecker-structured measurement matrices. Finally, our analysis is further extended to the Kronecker product of more than two matrices.

Convergence of Expectation-Maximization Algorithm with Mixed-Integer Optimization

The convergence of expectation-maximization (EM)-based algorithms typically requires continuity of the likelihood function with respect to all the unknown parameters (optimization variables). The requirement is not met when parameters comprise both discrete and continuous variables, making the convergence analysis nontrivial. This paper introduces a set of conditions that ensure the convergence of a specific class of EM algorithms that estimate a mixture of discrete and continuous parameters. Our results offer a new analysis technique for iterative algorithms that solve mixed-integer non-linear optimization problems. As a concrete example, we prove the convergence of the EM-based sparse Bayesian learning algorithm in [1] that estimates the state of a linear dynamical system with jointly sparse inputs and bursty missing observations. Our results establish that the algorithm in [1] converges to the set of stationary points of the maximum likelihood cost with respect to the continuous optimization variables.

Joint State and Input Estimation for Linear Dynamical Systems with Sparse Control

Sparsity constraints on the control inputs of a linear dynamical system naturally arise in several practical applications such as networked control, computer vision, seismic signal processing, and cyber-physical systems. In this work, we consider the problem of jointly estimating the states and sparse inputs of such systems from low-dimensional (compressive) measurements. Due to the low-dimensional measurements, conventional Kalman filtering and smoothing algorithms fail to accurately estimate the states and inputs. We present a Bayesian approach that exploits the input sparsity to significantly improve estimation accuracy. Sparsity in the input estimates is promoted by using different prior distributions on the input. We investigate two main approaches: regularizer-based MAP, and {Bayesian learning-based estimation}. We also extend the approaches to handle control inputs with common support and analyze the time and memory complexities of the presented algorithms. Finally, using numerical simulations, we show that our algorithms outperform the state-of-the-art methods in terms of accuracy and time/memory complexities, especially in the low-dimensional measurement regime.

Anomaly Detection via Learning-Based Sequential Controlled Sensing

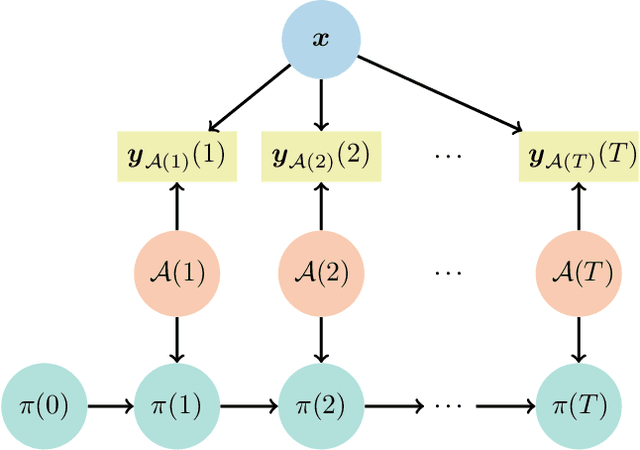
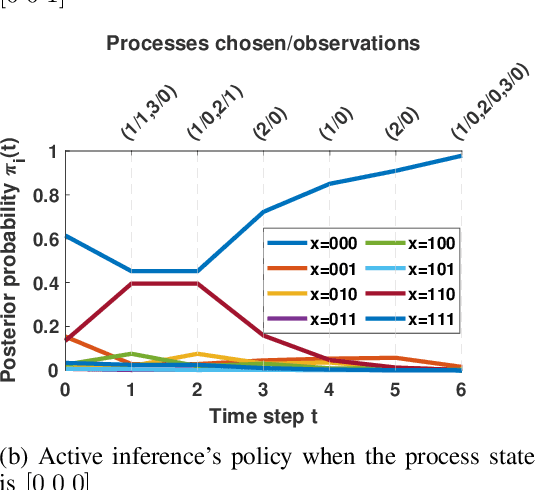
In this paper, we address the problem of detecting anomalies among a given set of binary processes via learning-based controlled sensing. Each process is parameterized by a binary random variable indicating whether the process is anomalous. To identify the anomalies, the decision-making agent is allowed to observe a subset of the processes at each time instant. Also, probing each process has an associated cost. Our objective is to design a sequential selection policy that dynamically determines which processes to observe at each time with the goal to minimize the delay in making the decision and the total sensing cost. We cast this problem as a sequential hypothesis testing problem within the framework of Markov decision processes. This formulation utilizes both a Bayesian log-likelihood ratio-based reward and an entropy-based reward. The problem is then solved using two approaches: 1) a deep reinforcement learning-based approach where we design both deep Q-learning and policy gradient actor-critic algorithms; and 2) a deep active inference-based approach. Using numerical experiments, we demonstrate the efficacy of our algorithms and show that our algorithms adapt to any unknown statistical dependence pattern of the processes.

Kronecker-structured Sparse Vector Recovery with Application to IRS-MIMO Channel Estimation

This paper studies the problem of Kronecker-structured sparse vector recovery from an underdetermined linear system with a Kronecker-structured dictionary. Such a problem arises in many real-world applications such as the sparse channel estimation of an intelligent reflecting surface-aided multiple-input multiple-output system. The prior art only exploits the Kronecker structure in the support of the sparse vector and solves the entire linear system together leading to high computational complexity. Instead, we break down the original sparse recovery problem into multiple independent sub-problems and solve them individually. We obtain the sparse vector as the Kronecker product of the individual solutions, retaining its structure in both support and nonzero entries. Our simulations demonstrate the superior performance of our methods in terms of accuracy and run time compared with the existing works, using synthetic data and the channel estimation application. We attribute the low run time to the reduced solution space due to the additional structure and improved accuracy to the denoising effect owing to the decomposition step.

Sparse Millimeter Wave Channel Estimation From Partially Coherent Measurements

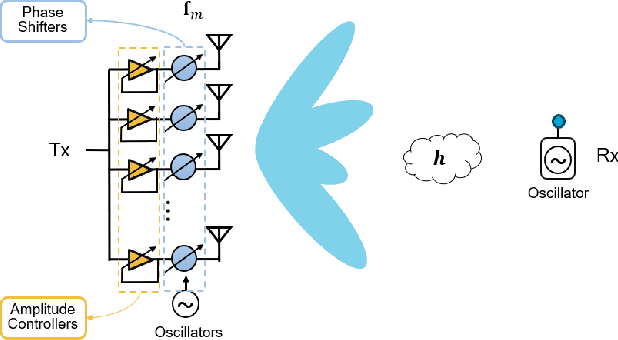
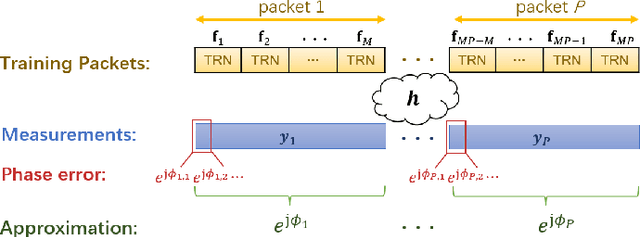
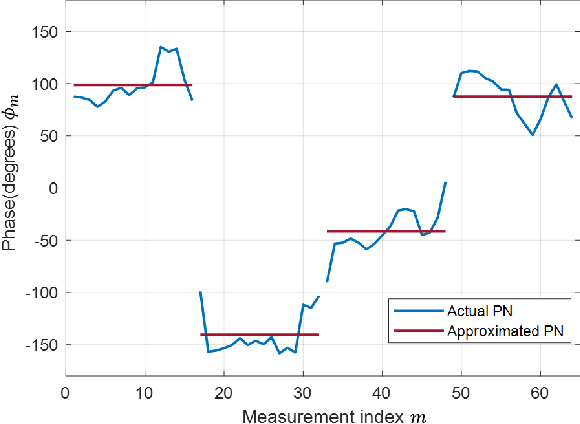
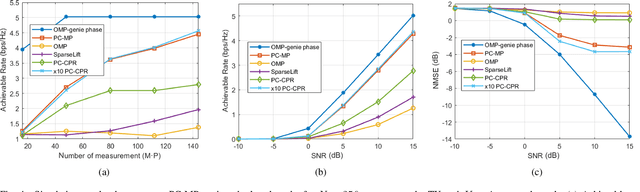
This paper develops a channel estimation technique for millimeter wave (mmWave) communication systems. Our method exploits the sparse structure in mmWave channels for low training overhead and accounts for the phase errors in the channel measurements due to phase noise at the oscillator. Specifically, in IEEE 802.11ad/ay-based mmWave systems, the phase errors within a beam refinement protocol packet are almost the same, while the errors across different packets are substantially different. Consequently, standard sparsity-aware algorithms, which ignore phase errors, fail when channel measurements are acquired over multiple beam refinement protocol packets. We present a novel algorithm called partially coherent matching pursuit for sparse channel estimation under practical phase noise perturbations. Our method iteratively detects the support of sparse signal and employs alternating minimization to jointly estimate the signal and the phase errors. We numerically show that our algorithm can reconstruct the channel accurately at a lower complexity than the benchmarks.

Bayesian Algorithms for Kronecker-structured Sparse Vector Recovery With Application to IRS-MIMO Channel Estimation

We study the sparse recovery problem with an underdetermined linear system characterized by a Kronecker-structured dictionary and a Kronecker-supported sparse vector. We cast this problem into the sparse Bayesian learning (SBL) framework and rely on the expectation-maximization method for a solution. To this end, we model the Kronecker-structured support with a hierarchical Gaussian prior distribution parameterized by a Kronecker-structured hyperparameter, leading to a non-convex optimization problem. The optimization problem is solved using the alternating minimization (AM) method and a singular value decomposition (SVD)-based method, resulting in two algorithms. Further, we analytically guarantee that the AM-based method converges to the stationary point of the SBL cost function. The SVD-based method, though it adopts approximations, is empirically shown to be more efficient and accurate. We then apply our algorithm to estimate the uplink wireless channel in an intelligent reflecting surface-aided MIMO system and extend the AM-based algorithm to address block sparsity in the channel. We also study the SBL cost to show that the minima of the cost function are achieved at sparse solutions and that incorporating the Kronecker structure reduces the number of local minima of the SBL cost function. Our numerical results demonstrate the effectiveness of our algorithms compared to the state-of-the-art.