Efficient Off-Grid Bayesian Parameter Estimation for Kronecker-Structured Signals

This work studies the problem of jointly estimating unknown parameters from Kronecker-structured multidimensional signals, which arises in applications like intelligent reflecting surface (IRS)-aided channel estimation. Exploiting the Kronecker structure, we decompose the estimation problem into smaller, independent subproblems across each dimension. Each subproblem is posed as a sparse recovery problem using basis expansion and solved using a novel off-grid sparse Bayesian learning (SBL)-based algorithm. Additionally, we derive probabilistic error bounds for the decomposition, quantify its denoising effect, and provide convergence analysis for off-grid SBL. Our simulations show that applying the algorithm to IRS-aided channel estimation improves accuracy and runtime compared to state-of-the-art methods through the low-complexity and denoising benefits of the decomposition step and the high-resolution estimation capabilities of off-grid SBL.

On the Restricted Isometry Property of Kronecker-structured Matrices

In this work, we study the restricted isometry property (RIP) of Kronecker-structured matrices, formed by the Kronecker product of two factor matrices. Previously, only upper and lower bounds on the restricted isometry constant (RIC) in terms of the RICs of the factor matrices were known. We derive a probabilistic measurement bound for the $s$th-order RIC. We show that the Kronecker product of two sub-Gaussian matrices satisfies RIP with high probability if the minimum number of rows among two matrices is $\mathcal{O}(s \ln \max\{N_1, N_2\})$. Here, $s$ is the sparsity level, and $N_1$ and $N_2$ are the number of columns in the matrices. We also present improved measurement bounds for the recovery of Kronecker-structured sparse vectors using Kronecker-structured measurement matrices. Finally, our analysis is further extended to the Kronecker product of more than two matrices.

Kronecker-structured Sparse Vector Recovery with Application to IRS-MIMO Channel Estimation

This paper studies the problem of Kronecker-structured sparse vector recovery from an underdetermined linear system with a Kronecker-structured dictionary. Such a problem arises in many real-world applications such as the sparse channel estimation of an intelligent reflecting surface-aided multiple-input multiple-output system. The prior art only exploits the Kronecker structure in the support of the sparse vector and solves the entire linear system together leading to high computational complexity. Instead, we break down the original sparse recovery problem into multiple independent sub-problems and solve them individually. We obtain the sparse vector as the Kronecker product of the individual solutions, retaining its structure in both support and nonzero entries. Our simulations demonstrate the superior performance of our methods in terms of accuracy and run time compared with the existing works, using synthetic data and the channel estimation application. We attribute the low run time to the reduced solution space due to the additional structure and improved accuracy to the denoising effect owing to the decomposition step.

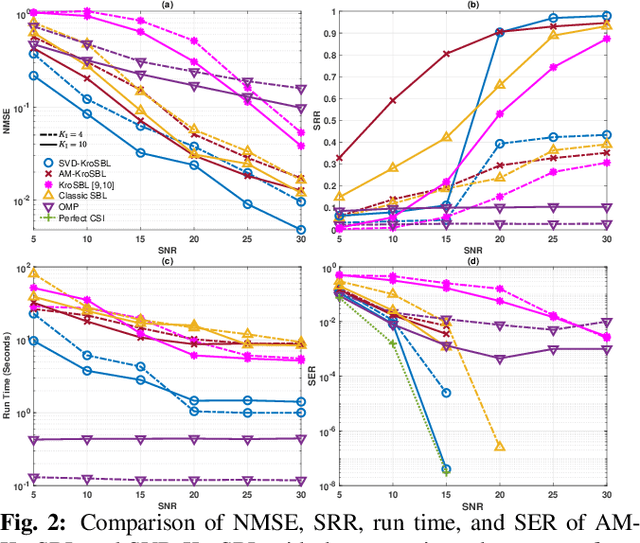
Bayesian Algorithms for Kronecker-structured Sparse Vector Recovery With Application to IRS-MIMO Channel Estimation

We study the sparse recovery problem with an underdetermined linear system characterized by a Kronecker-structured dictionary and a Kronecker-supported sparse vector. We cast this problem into the sparse Bayesian learning (SBL) framework and rely on the expectation-maximization method for a solution. To this end, we model the Kronecker-structured support with a hierarchical Gaussian prior distribution parameterized by a Kronecker-structured hyperparameter, leading to a non-convex optimization problem. The optimization problem is solved using the alternating minimization (AM) method and a singular value decomposition (SVD)-based method, resulting in two algorithms. Further, we analytically guarantee that the AM-based method converges to the stationary point of the SBL cost function. The SVD-based method, though it adopts approximations, is empirically shown to be more efficient and accurate. We then apply our algorithm to estimate the uplink wireless channel in an intelligent reflecting surface-aided MIMO system and extend the AM-based algorithm to address block sparsity in the channel. We also study the SBL cost to show that the minima of the cost function are achieved at sparse solutions and that incorporating the Kronecker structure reduces the number of local minima of the SBL cost function. Our numerical results demonstrate the effectiveness of our algorithms compared to the state-of-the-art.

Structure-aware Sparse Bayesian Learning-based Channel Estimation for Intelligent Reflecting Surface-aided MIMO

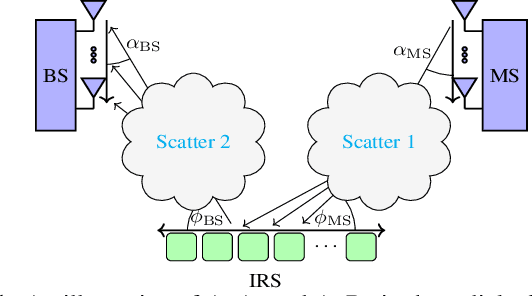
This paper presents novel cascaded channel estimation techniques for an intelligent reflecting surface-aided multiple-input multiple-output system. Motivated by the channel angular sparsity at higher frequency bands, the channel estimation problem is formulated as a sparse vector recovery problem with an inherent Kronecker structure. We solve the problem using the sparse Bayesian learning framework which leads to a non-convex optimization problem. We offer two solution techniques to the problem based on alternating minimization and singular value decomposition. Our simulation results illustrate the superior performance of our methods in terms of accuracy and run time compared with the existing works.

A channel attention based MLP-Mixer network for motor imagery decoding with EEG

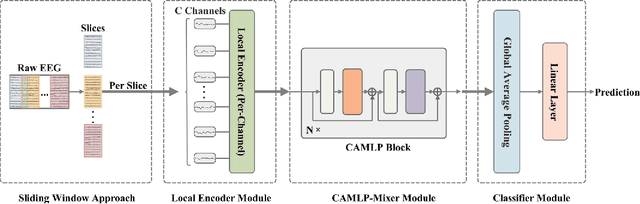
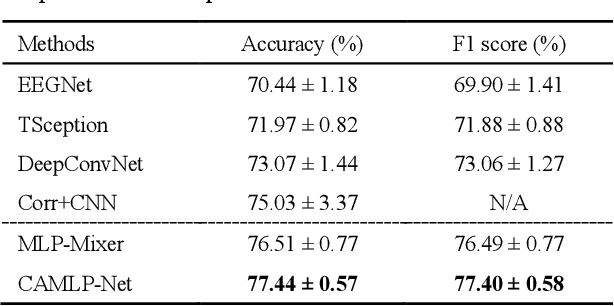
Convolutional neural networks (CNNs) and their variants have been successfully applied to the electroencephalogram (EEG) based motor imagery (MI) decoding task. However, these CNN-based algorithms generally have limitations in perceiving global temporal dependencies of EEG signals. Besides, they also ignore the diverse contributions of different EEG channels to the classification task. To address such issues, a novel channel attention based MLP-Mixer network (CAMLP-Net) is proposed for EEG-based MI decoding. Specifically, the MLP-based architecture is applied in this network to capture the temporal and spatial information. The attention mechanism is further embedded into MLP-Mixer to adaptively exploit the importance of different EEG channels. Therefore, the proposed CAMLP-Net can effectively learn more global temporal and spatial information. The experimental results on the newly built MI-2 dataset indicate that our proposed CAMLP-Net achieves superior classification performance over all the compared algorithms.