Multiscale Low-Frequency Memory Network for Improved Feature Extraction in Convolutional Neural Networks

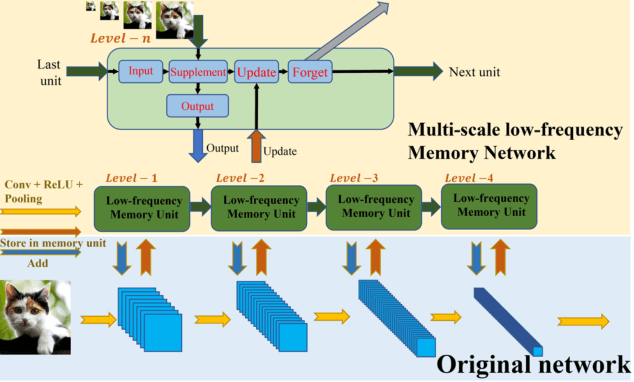
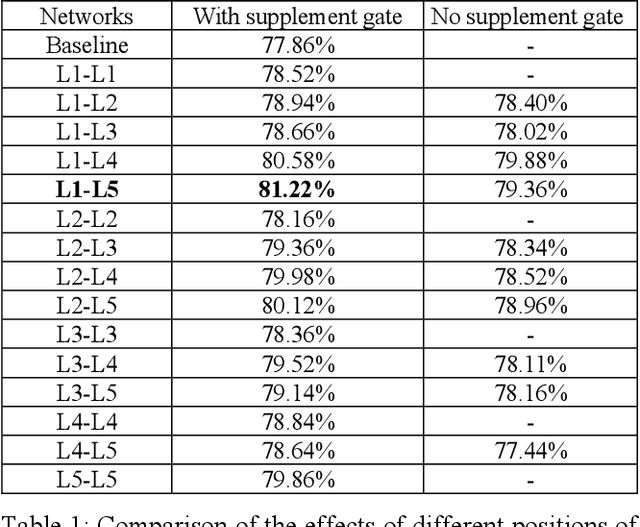
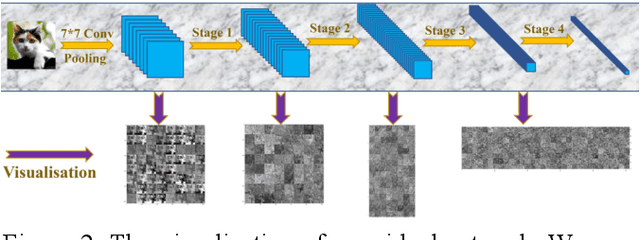
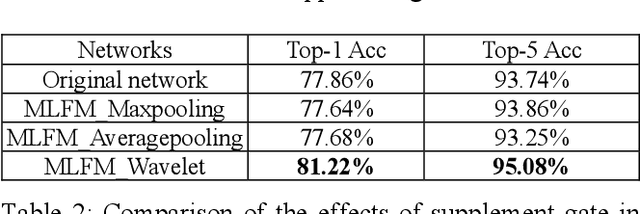
Deep learning and Convolutional Neural Networks (CNNs) have driven major transformations in diverse research areas. However, their limitations in handling low-frequency information present obstacles in certain tasks like interpreting global structures or managing smooth transition images. Despite the promising performance of transformer structures in numerous tasks, their intricate optimization complexities highlight the persistent need for refined CNN enhancements using limited resources. Responding to these complexities, we introduce a novel framework, the Multiscale Low-Frequency Memory (MLFM) Network, with the goal to harness the full potential of CNNs while keeping their complexity unchanged. The MLFM efficiently preserves low-frequency information, enhancing performance in targeted computer vision tasks. Central to our MLFM is the Low-Frequency Memory Unit (LFMU), which stores various low-frequency data and forms a parallel channel to the core network. A key advantage of MLFM is its seamless compatibility with various prevalent networks, requiring no alterations to their original core structure. Testing on ImageNet demonstrated substantial accuracy improvements in multiple 2D CNNs, including ResNet, MobileNet, EfficientNet, and ConvNeXt. Furthermore, we showcase MLFM's versatility beyond traditional image classification by successfully integrating it into image-to-image translation tasks, specifically in semantic segmentation networks like FCN and U-Net. In conclusion, our work signifies a pivotal stride in the journey of optimizing the efficacy and efficiency of CNNs with limited resources. This research builds upon the existing CNN foundations and paves the way for future advancements in computer vision. Our codes are available at https://github.com/AlphaWuSeu/ MLFM.

Generative networks as inverse problems with fractional wavelet scattering networks

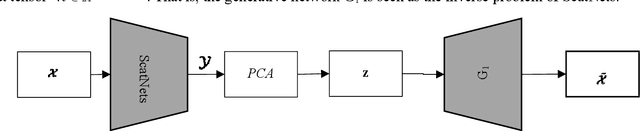
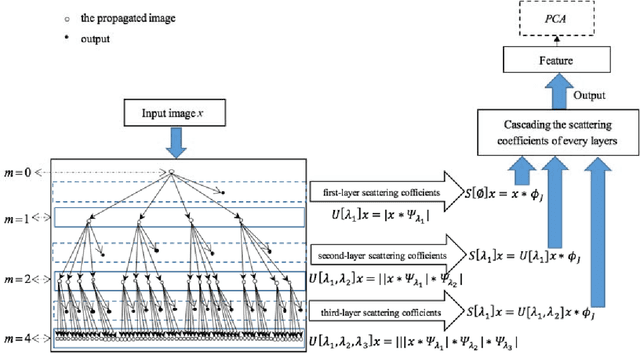
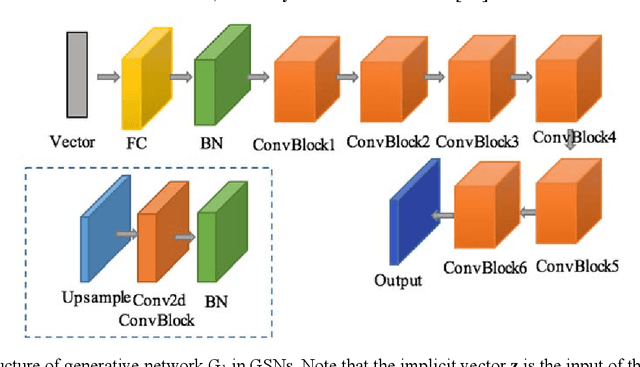
Deep learning is a hot research topic in the field of machine learning methods and applications. Generative Adversarial Networks (GANs) and Variational Auto-Encoders (VAEs) provide impressive image generations from Gaussian white noise, but both of them are difficult to train since they need to train the generator (or encoder) and the discriminator (or decoder) simultaneously, which is easy to cause unstable training. In order to solve or alleviate the synchronous training difficult problems of GANs and VAEs, recently, researchers propose Generative Scattering Networks (GSNs), which use wavelet scattering networks (ScatNets) as the encoder to obtain the features (or ScatNet embeddings) and convolutional neural networks (CNNs) as the decoder to generate the image. The advantage of GSNs is the parameters of ScatNets are not needed to learn, and the disadvantage of GSNs is that the expression ability of ScatNets is slightly weaker than CNNs and the dimensional reduction method of Principal Component Analysis (PCA) is easy to lead overfitting in the training of GSNs, and therefore affect the generated quality in the testing process. In order to further improve the quality of generated images while keep the advantages of GSNs, this paper proposes Generative Fractional Scattering Networks (GFRSNs), which use more expressive fractional wavelet scattering networks (FrScatNets) instead of ScatNets as the encoder to obtain the features (or FrScatNet embeddings) and use the similar CNNs of GSNs as the decoder to generate the image. Additionally, this paper develops a new dimensional reduction method named Feature-Map Fusion (FMF) instead of PCA for better keeping the information of FrScatNets and the effect of image fusion on the quality of image generation is also discussed.

Fractional spectral graph wavelets and their applications

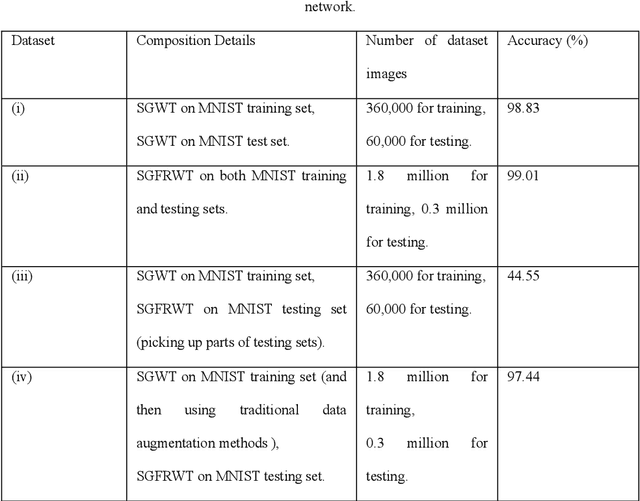
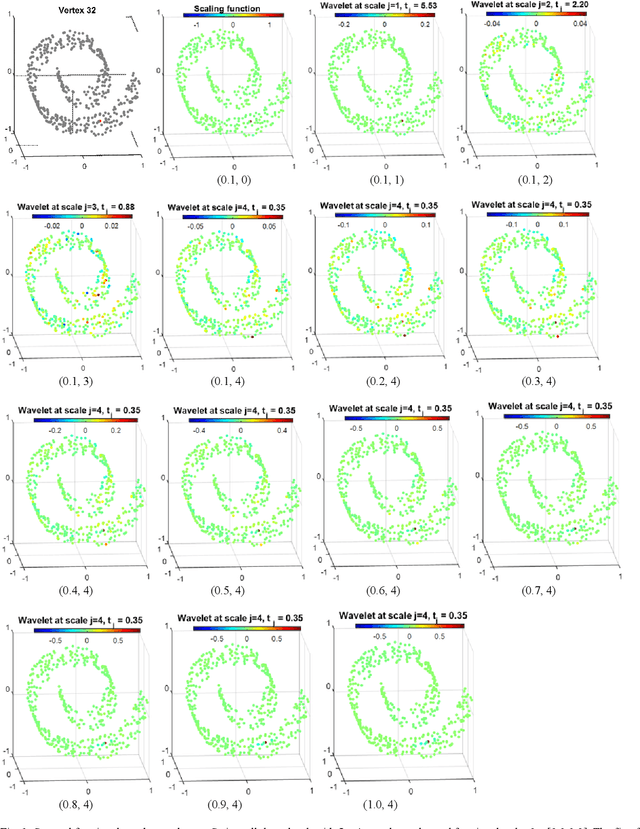
One of the key challenges in the area of signal processing on graphs is to design transforms and dictionaries methods to identify and exploit structure in signals on weighted graphs. In this paper, we first generalize graph Fourier transform (GFT) to graph fractional Fourier transform (GFRFT), which is then used to define a novel transform named spectral graph fractional wavelet transform (SGFRWT), which is a generalized and extended version of spectral graph wavelet transform (SGWT). A fast algorithm for SGFRWT is also derived and implemented based on Fourier series approximation. The potential applications of SGFRWT are also presented.