Fred Hamprecht
HCI
Visualizing hierarchies in scRNA-seq data using a density tree-biased autoencoder
Feb 11, 2021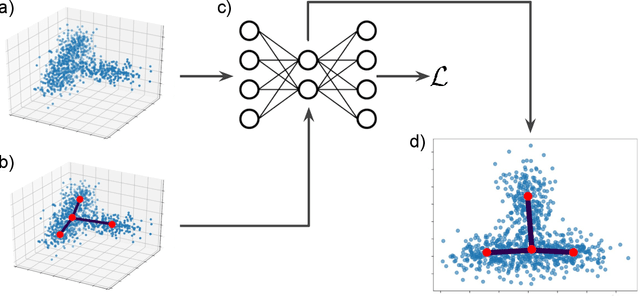
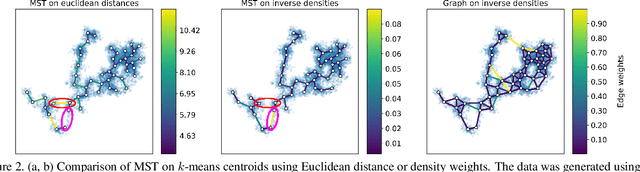
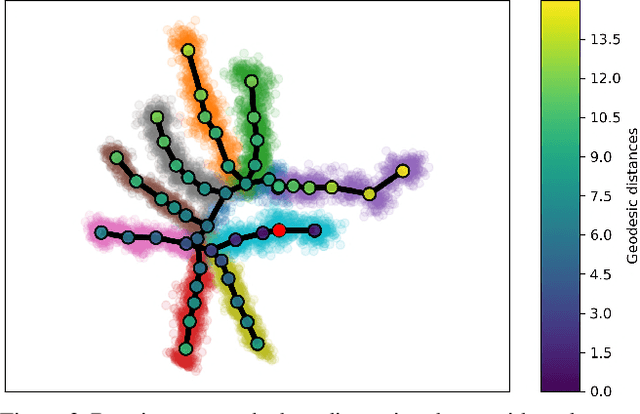
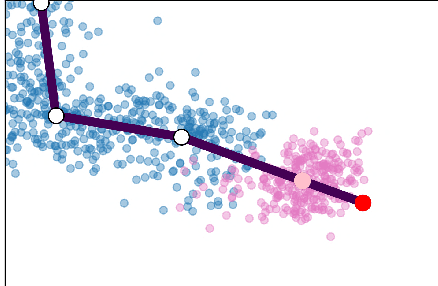
Abstract:Single cell RNA sequencing (scRNA-seq) data makes studying the development of cells possible at unparalleled resolution. Given that many cellular differentiation processes are hierarchical, their scRNA-seq data is expected to be approximately tree-shaped in gene expression space. Inference and representation of this tree-structure in two dimensions is highly desirable for biological interpretation and exploratory analysis. Our two contributions are an approach for identifying a meaningful tree structure from high-dimensional scRNA-seq data, and a visualization method respecting the tree-structure. We extract the tree structure by means of a density based minimum spanning tree on a vector quantization of the data and show that it captures biological information well. We then introduce DTAE, a tree-biased autoencoder that emphasizes the tree structure of the data in low dimensional space. We compare to other dimension reduction methods and demonstrate the success of our method experimentally. Our implementation relying on PyTorch and Higra is available at github.com/hci-unihd/DTAE.
Learned Watershed: End-to-End Learning of Seeded Segmentation
Sep 04, 2017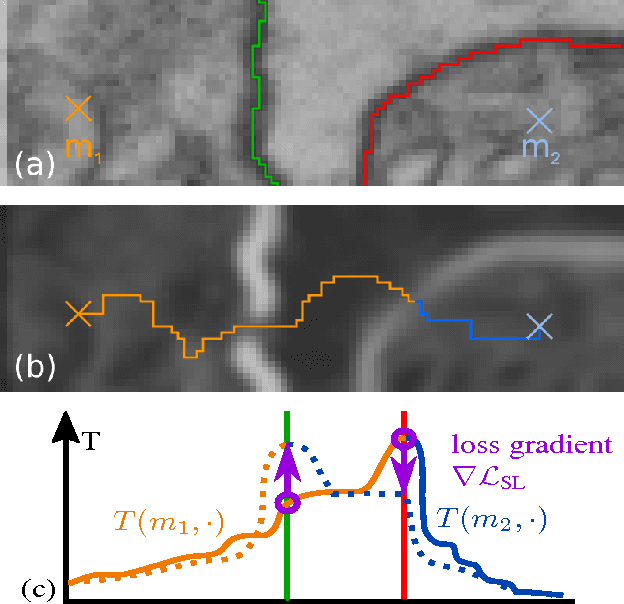
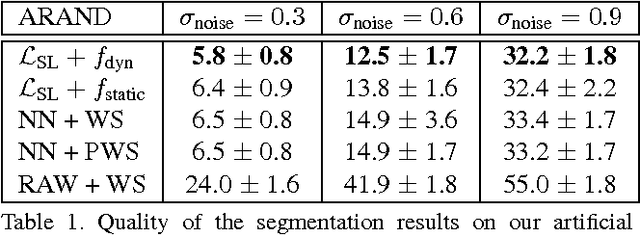

Abstract:Learned boundary maps are known to outperform hand- crafted ones as a basis for the watershed algorithm. We show, for the first time, how to train watershed computation jointly with boundary map prediction. The estimator for the merging priorities is cast as a neural network that is con- volutional (over space) and recurrent (over iterations). The latter allows learning of complex shape priors. The method gives the best known seeded segmentation results on the CREMI segmentation challenge.
Structured Learning from Partial Annotations
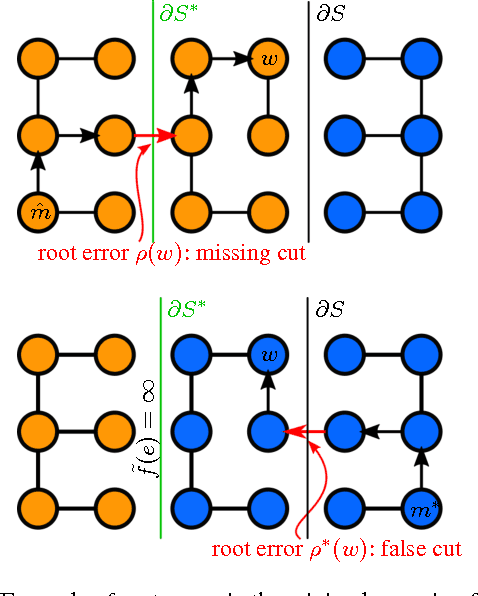
Jun 27, 2012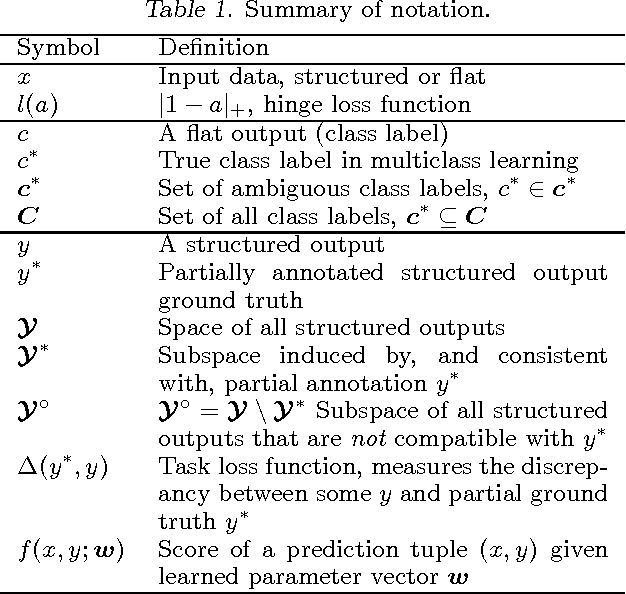
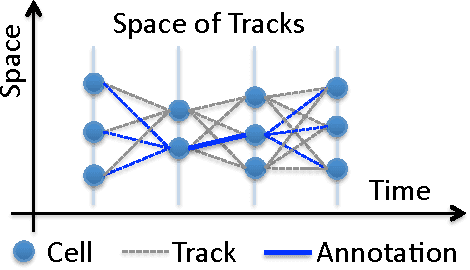

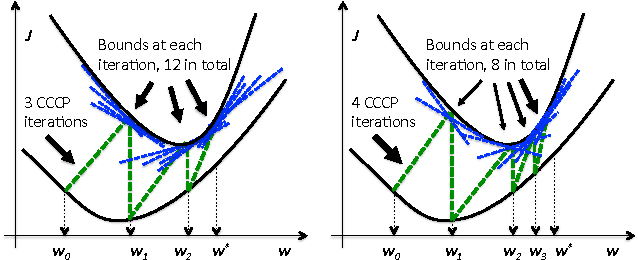
Abstract:Structured learning is appropriate when predicting structured outputs such as trees, graphs, or sequences. Most prior work requires the training set to consist of complete trees, graphs or sequences. Specifying such detailed ground truth can be tedious or infeasible for large outputs. Our main contribution is a large margin formulation that makes structured learning from only partially annotated data possible. The resulting optimization problem is non-convex, yet can be efficiently solve by concave-convex procedure (CCCP) with novel speedup strategies. We apply our method to a challenging tracking-by-assignment problem of a variable number of divisible objects. On this benchmark, using only 25% of a full annotation we achieve a performance comparable to a model learned with a full annotation. Finally, we offer a unifying perspective of previous work using the hinge, ramp, or max loss for structured learning, followed by an empirical comparison on their practical performance.
Multi-Hypothesis CRF-Segmentation of Neural Tissue in Anisotropic EM Volumes
Sep 18, 2011



Abstract:We present an approach for the joint segmentation and grouping of similar components in anisotropic 3D image data and use it to segment neural tissue in serial sections electron microscopy (EM) images. We first construct a nested set of neuron segmentation hypotheses for each slice. A conditional random field (CRF) then allows us to evaluate both the compatibility of a specific segmentation and a specific inter-slice assignment of neuron candidates with the underlying observations. The model is solved optimally for an entire image stack simultaneously using integer linear programming (ILP), which yields the maximum a posteriori solution in amortized linear time in the number of slices. We evaluate the performance of our approach on an annotated sample of the Drosophila larva neuropil and show that the consideration of different segmentation hypotheses in each slice leads to a significant improvement in the segmentation and assignment accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge