Learning Negative Mixture Models by Tensor Decompositions

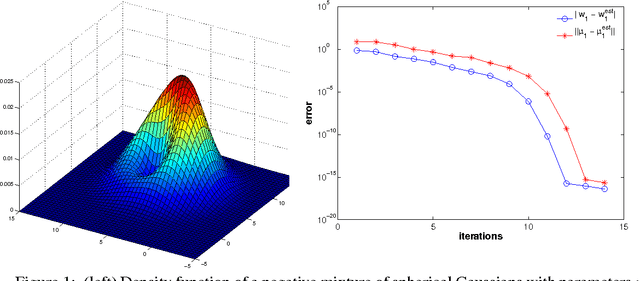
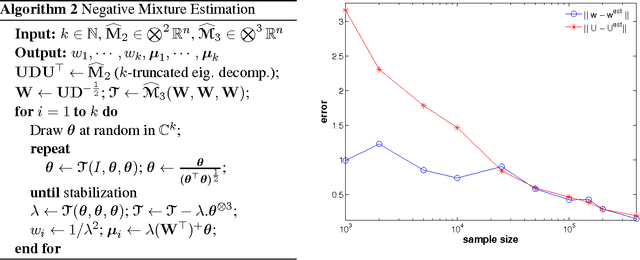
This work considers the problem of estimating the parameters of negative mixture models, i.e. mixture models that possibly involve negative weights. The contributions of this paper are as follows. (i) We show that every rational probability distributions on strings, a representation which occurs naturally in spectral learning, can be computed by a negative mixture of at most two probabilistic automata (or HMMs). (ii) We propose a method to estimate the parameters of negative mixture models having a specific tensor structure in their low order observable moments. Building upon a recent paper on tensor decompositions for learning latent variable models, we extend this work to the broader setting of tensors having a symmetric decomposition with positive and negative weights. We introduce a generalization of the tensor power method for complex valued tensors, and establish theoretical convergence guarantees. (iii) We show how our approach applies to negative Gaussian mixture models, for which we provide some experiments.

Dimension-free Concentration Bounds on Hankel Matrices for Spectral Learning

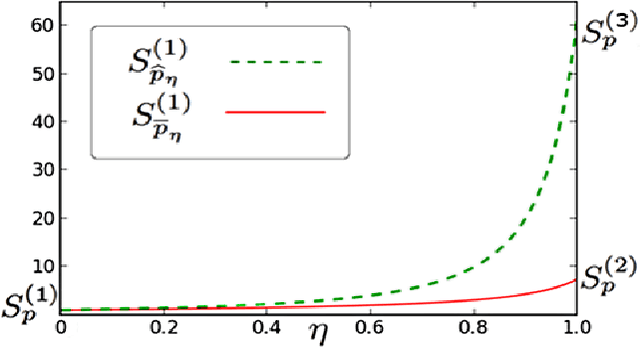
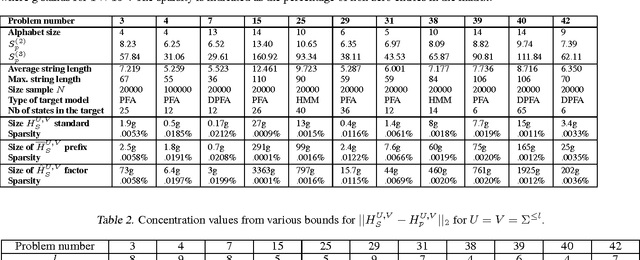
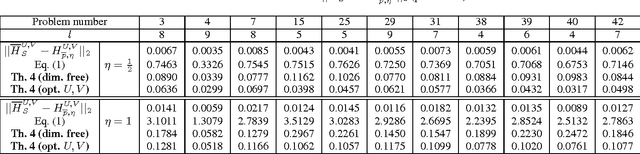
Learning probabilistic models over strings is an important issue for many applications. Spectral methods propose elegant solutions to the problem of inferring weighted automata from finite samples of variable-length strings drawn from an unknown target distribution. These methods rely on a singular value decomposition of a matrix $H_S$, called the Hankel matrix, that records the frequencies of (some of) the observed strings. The accuracy of the learned distribution depends both on the quantity of information embedded in $H_S$ and on the distance between $H_S$ and its mean $H_r$. Existing concentration bounds seem to indicate that the concentration over $H_r$ gets looser with the size of $H_r$, suggesting to make a trade-off between the quantity of used information and the size of $H_r$. We propose new dimension-free concentration bounds for several variants of Hankel matrices. Experiments demonstrate that these bounds are tight and that they significantly improve existing bounds. These results suggest that the concentration rate of the Hankel matrix around its mean does not constitute an argument for limiting its size.

On Probability Distributions for Trees: Representations, Inference and Learning

We study probability distributions over free algebras of trees. Probability distributions can be seen as particular (formal power) tree series [Berstel et al 82, Esik et al 03], i.e. mappings from trees to a semiring K . A widely studied class of tree series is the class of rational (or recognizable) tree series which can be defined either in an algebraic way or by means of multiplicity tree automata. We argue that the algebraic representation is very convenient to model probability distributions over a free algebra of trees. First, as in the string case, the algebraic representation allows to design learning algorithms for the whole class of probability distributions defined by rational tree series. Note that learning algorithms for rational tree series correspond to learning algorithms for weighted tree automata where both the structure and the weights are learned. Second, the algebraic representation can be easily extended to deal with unranked trees (like XML trees where a symbol may have an unbounded number of children). Both properties are particularly relevant for applications: nondeterministic automata are required for the inference problem to be relevant (recall that Hidden Markov Models are equivalent to nondeterministic string automata); nowadays applications for Web Information Extraction, Web Services and document processing consider unranked trees.

Rational stochastic languages

The goal of the present paper is to provide a systematic and comprehensive study of rational stochastic languages over a semiring K \in {Q, Q +, R, R+}. A rational stochastic language is a probability distribution over a free monoid \Sigma^* which is rational over K, that is which can be generated by a multiplicity automata with parameters in K. We study the relations between the classes of rational stochastic languages S rat K (\Sigma). We define the notion of residual of a stochastic language and we use it to investigate properties of several subclasses of rational stochastic languages. Lastly, we study the representation of rational stochastic languages by means of multiplicity automata.

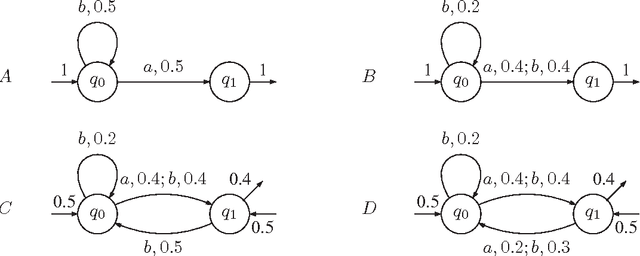
Learning rational stochastic languages

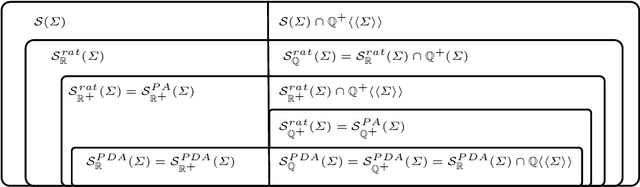
Given a finite set of words w1,...,wn independently drawn according to a fixed unknown distribution law P called a stochastic language, an usual goal in Grammatical Inference is to infer an estimate of P in some class of probabilistic models, such as Probabilistic Automata (PA). Here, we study the class of rational stochastic languages, which consists in stochastic languages that can be generated by Multiplicity Automata (MA) and which strictly includes the class of stochastic languages generated by PA. Rational stochastic languages have minimal normal representation which may be very concise, and whose parameters can be efficiently estimated from stochastic samples. We design an efficient inference algorithm DEES which aims at building a minimal normal representation of the target. Despite the fact that no recursively enumerable class of MA computes exactly the set of rational stochastic languages over Q, we show that DEES strongly identifies tis set in the limit. We study the intermediary MA output by DEES and show that they compute rational series which converge absolutely to one and which can be used to provide stochastic languages which closely estimate the target.