Learning Negative Mixture Models by Tensor Decompositions
Paper and Code
Sep 19, 2014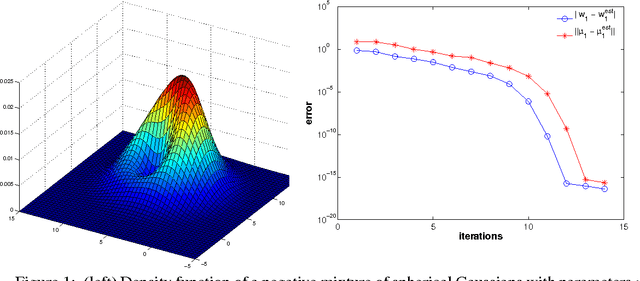
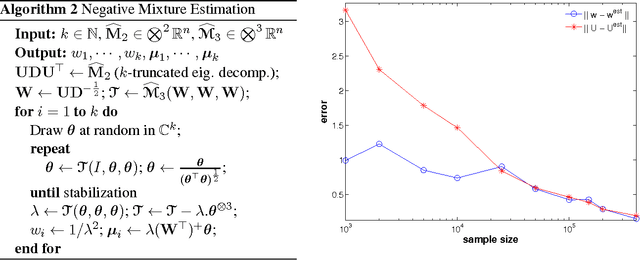
This work considers the problem of estimating the parameters of negative mixture models, i.e. mixture models that possibly involve negative weights. The contributions of this paper are as follows. (i) We show that every rational probability distributions on strings, a representation which occurs naturally in spectral learning, can be computed by a negative mixture of at most two probabilistic automata (or HMMs). (ii) We propose a method to estimate the parameters of negative mixture models having a specific tensor structure in their low order observable moments. Building upon a recent paper on tensor decompositions for learning latent variable models, we extend this work to the broader setting of tensors having a symmetric decomposition with positive and negative weights. We introduce a generalization of the tensor power method for complex valued tensors, and establish theoretical convergence guarantees. (iii) We show how our approach applies to negative Gaussian mixture models, for which we provide some experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge