Rational stochastic languages

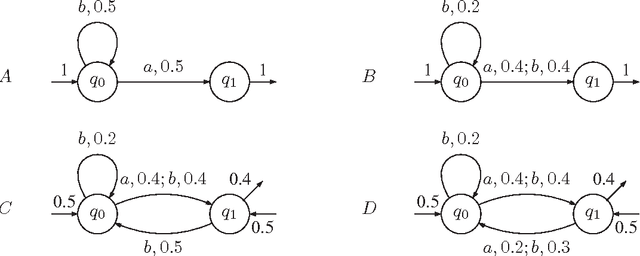
The goal of the present paper is to provide a systematic and comprehensive study of rational stochastic languages over a semiring K \in {Q, Q +, R, R+}. A rational stochastic language is a probability distribution over a free monoid \Sigma^* which is rational over K, that is which can be generated by a multiplicity automata with parameters in K. We study the relations between the classes of rational stochastic languages S rat K (\Sigma). We define the notion of residual of a stochastic language and we use it to investigate properties of several subclasses of rational stochastic languages. Lastly, we study the representation of rational stochastic languages by means of multiplicity automata.