Using Pseudo-Stochastic Rational Languages in Probabilistic Grammatical Inference

In probabilistic grammatical inference, a usual goal is to infer a good approximation of an unknown distribution P called a stochastic language. The estimate of P stands in some class of probabilistic models such as probabilistic automata (PA). In this paper, we focus on probabilistic models based on multiplicity automata (MA). The stochastic languages generated by MA are called rational stochastic languages; they strictly include stochastic languages generated by PA; they also admit a very concise canonical representation. Despite the fact that this class is not recursively enumerable, it is efficiently identifiable in the limit by using the algorithm DEES, introduced by the authors in a previous paper. However, the identification is not proper and before the convergence of the algorithm, DEES can produce MA that do not define stochastic languages. Nevertheless, it is possible to use these MA to define stochastic languages. We show that they belong to a broader class of rational series, that we call pseudo-stochastic rational languages. The aim of this paper is twofold. First we provide a theoretical study of pseudo-stochastic rational languages, the languages output by DEES, showing for example that this class is decidable within polynomial time. Second, we have carried out a lot of experiments in order to compare DEES to classical inference algorithms such as ALERGIA and MDI. They show that DEES outperforms them in most cases.

Rational stochastic languages

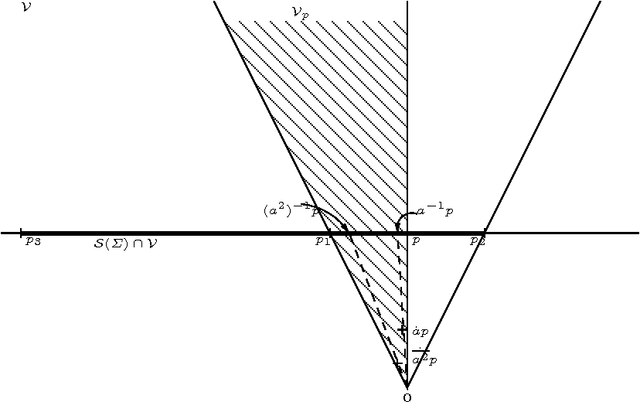
The goal of the present paper is to provide a systematic and comprehensive study of rational stochastic languages over a semiring K \in {Q, Q +, R, R+}. A rational stochastic language is a probability distribution over a free monoid \Sigma^* which is rational over K, that is which can be generated by a multiplicity automata with parameters in K. We study the relations between the classes of rational stochastic languages S rat K (\Sigma). We define the notion of residual of a stochastic language and we use it to investigate properties of several subclasses of rational stochastic languages. Lastly, we study the representation of rational stochastic languages by means of multiplicity automata.

Learning rational stochastic languages

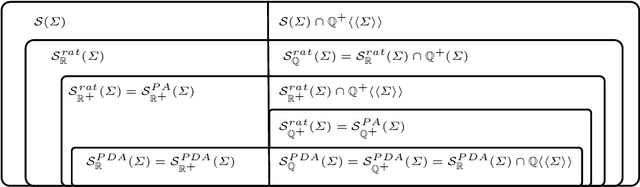
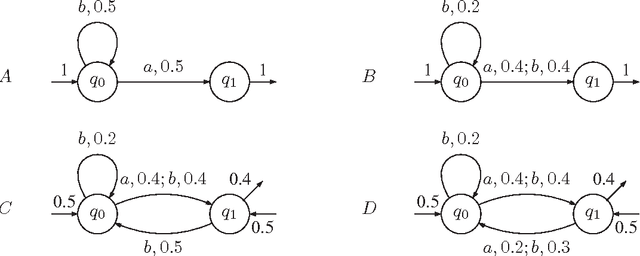
Given a finite set of words w1,...,wn independently drawn according to a fixed unknown distribution law P called a stochastic language, an usual goal in Grammatical Inference is to infer an estimate of P in some class of probabilistic models, such as Probabilistic Automata (PA). Here, we study the class of rational stochastic languages, which consists in stochastic languages that can be generated by Multiplicity Automata (MA) and which strictly includes the class of stochastic languages generated by PA. Rational stochastic languages have minimal normal representation which may be very concise, and whose parameters can be efficiently estimated from stochastic samples. We design an efficient inference algorithm DEES which aims at building a minimal normal representation of the target. Despite the fact that no recursively enumerable class of MA computes exactly the set of rational stochastic languages over Q, we show that DEES strongly identifies tis set in the limit. We study the intermediary MA output by DEES and show that they compute rational series which converge absolutely to one and which can be used to provide stochastic languages which closely estimate the target.