Beyond MSE: Ordinal Cross-Entropy for Probabilistic Time Series Forecasting

Time series forecasting is an important task that involves analyzing temporal dependencies and underlying patterns (such as trends, cyclicality, and seasonality) in historical data to predict future values or trends. Current deep learning-based forecasting models primarily employ Mean Squared Error (MSE) loss functions for regression modeling. Despite enabling direct value prediction, this method offers no uncertainty estimation and exhibits poor outlier robustness. To address these limitations, we propose OCE-TS, a novel ordinal classification approach for time series forecasting that replaces MSE with Ordinal Cross-Entropy (OCE) loss, preserving prediction order while quantifying uncertainty through probability output. Specifically, OCE-TS begins by discretizing observed values into ordered intervals and deriving their probabilities via a parametric distribution as supervision signals. Using a simple linear model, we then predict probability distributions for each timestep. The OCE loss is computed between the cumulative distributions of predicted and ground-truth probabilities, explicitly preserving ordinal relationships among forecasted values. Through theoretical analysis using influence functions, we establish that cross-entropy (CE) loss exhibits superior stability and outlier robustness compared to MSE loss. Empirically, we compared OCE-TS with five baseline models-Autoformer, DLinear, iTransformer, TimeXer, and TimeBridge-on seven public time series datasets. Using MSE and Mean Absolute Error (MAE) as evaluation metrics, the results demonstrate that OCE-TS consistently outperforms benchmark models. The code will be published.

RI-Loss: A Learnable Residual-Informed Loss for Time Series Forecasting

Time series forecasting relies on predicting future values from historical data, yet most state-of-the-art approaches-including transformer and multilayer perceptron-based models-optimize using Mean Squared Error (MSE), which has two fundamental weaknesses: its point-wise error computation fails to capture temporal relationships, and it does not account for inherent noise in the data. To overcome these limitations, we introduce the Residual-Informed Loss (RI-Loss), a novel objective function based on the Hilbert-Schmidt Independence Criterion (HSIC). RI-Loss explicitly models noise structure by enforcing dependence between the residual sequence and a random time series, enabling more robust, noise-aware representations. Theoretically, we derive the first non-asymptotic HSIC bound with explicit double-sample complexity terms, achieving optimal convergence rates through Bernstein-type concentration inequalities and Rademacher complexity analysis. This provides rigorous guarantees for RI-Loss optimization while precisely quantifying kernel space interactions. Empirically, experiments across eight real-world benchmarks and five leading forecasting models demonstrate improvements in predictive performance, validating the effectiveness of our approach. Code will be made publicly available to ensure reproducibility.

Hybrid Causal Identification and Causal Mechanism Clustering

Bivariate causal direction identification is a fundamental and vital problem in the causal inference field. Among binary causal methods, most methods based on additive noise only use one single causal mechanism to construct a causal model. In the real world, observations are always collected in different environments with heterogeneous causal relationships. Therefore, on observation data, this paper proposes a Mixture Conditional Variational Causal Inference model (MCVCI) to infer heterogeneous causality. Specifically, according to the identifiability of the Hybrid Additive Noise Model (HANM), MCVCI combines the superior fitting capabilities of the Gaussian mixture model and the neural network and elegantly uses the likelihoods obtained from the probabilistic bounds of the mixture conditional variational auto-encoder as causal decision criteria. Moreover, we model the casual heterogeneity into cluster numbers and propose the Mixture Conditional Variational Causal Clustering (MCVCC) method, which can reveal causal mechanism expression. Compared with state-of-the-art methods, the comprehensive best performance demonstrates the effectiveness of the methods proposed in this paper on several simulated and real data.

Sharper Error Bounds in Late Fusion Multi-view Clustering Using Eigenvalue Proportion

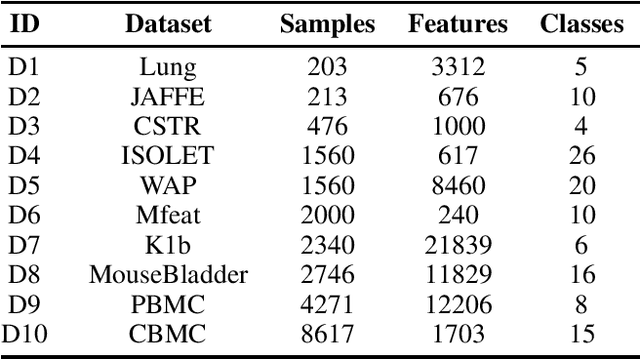
Multi-view clustering (MVC) aims to integrate complementary information from multiple views to enhance clustering performance. Late Fusion Multi-View Clustering (LFMVC) has shown promise by synthesizing diverse clustering results into a unified consensus. However, current LFMVC methods struggle with noisy and redundant partitions and often fail to capture high-order correlations across views. To address these limitations, we present a novel theoretical framework for analyzing the generalization error bounds of multiple kernel $k$-means, leveraging local Rademacher complexity and principal eigenvalue proportions. Our analysis establishes a convergence rate of $\mathcal{O}(1/n)$, significantly improving upon the existing rate in the order of $\mathcal{O}(\sqrt{k/n})$. Building on this insight, we propose a low-pass graph filtering strategy within a multiple linear $k$-means framework to mitigate noise and redundancy, further refining the principal eigenvalue proportion and enhancing clustering accuracy. Experimental results on benchmark datasets confirm that our approach outperforms state-of-the-art methods in clustering performance and robustness. The related codes is available at https://github.com/csliangdu/GMLKM .

k-HyperEdge Medoids for Clustering Ensemble

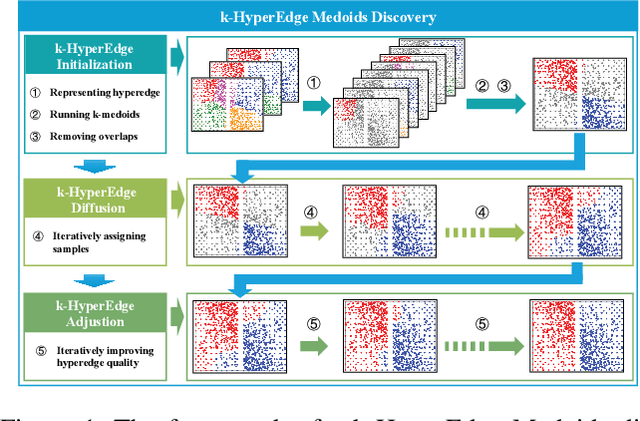
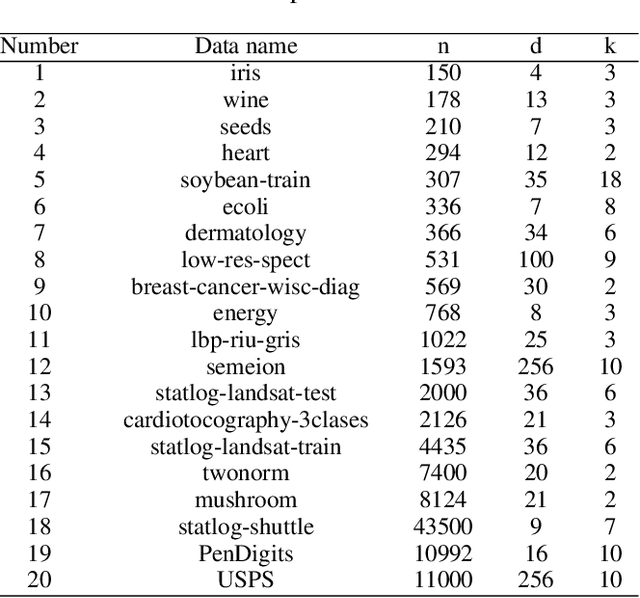
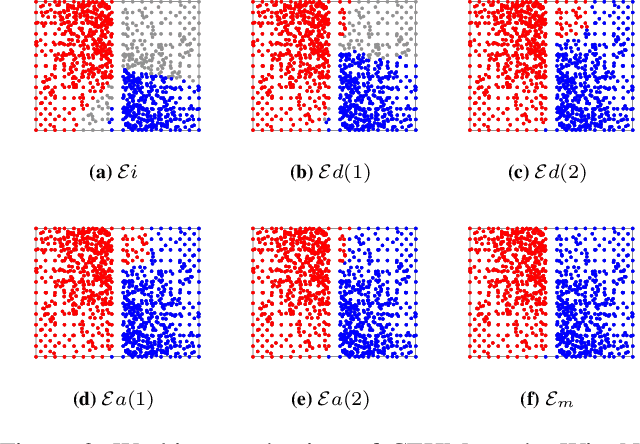
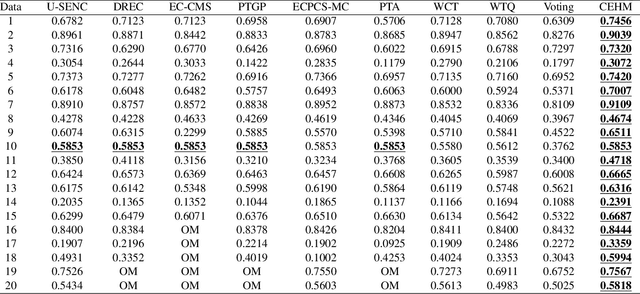
Clustering ensemble has been a popular research topic in data science due to its ability to improve the robustness of the single clustering method. Many clustering ensemble methods have been proposed, most of which can be categorized into clustering-view and sample-view methods. The clustering-view method is generally efficient, but it could be affected by the unreliability that existed in base clustering results. The sample-view method shows good performance, while the construction of the pairwise sample relation is time-consuming. In this paper, the clustering ensemble is formulated as a k-HyperEdge Medoids discovery problem and a clustering ensemble method based on k-HyperEdge Medoids that considers the characteristics of the above two types of clustering ensemble methods is proposed. In the method, a set of hyperedges is selected from the clustering view efficiently, then the hyperedges are diffused and adjusted from the sample view guided by a hyperedge loss function to construct an effective k-HyperEdge Medoid set. The loss function is mainly reduced by assigning samples to the hyperedge with the highest degree of belonging. Theoretical analyses show that the solution can approximate the optimal, the assignment method can gradually reduce the loss function, and the estimation of the belonging degree is statistically reasonable. Experiments on artificial data show the working mechanism of the proposed method. The convergence of the method is verified by experimental analysis of twenty data sets. The effectiveness and efficiency of the proposed method are also verified on these data, with nine representative clustering ensemble algorithms as reference.

Deep Embedding Clustering Driven by Sample Stability

Deep clustering methods improve the performance of clustering tasks by jointly optimizing deep representation learning and clustering. While numerous deep clustering algorithms have been proposed, most of them rely on artificially constructed pseudo targets for performing clustering. This construction process requires some prior knowledge, and it is challenging to determine a suitable pseudo target for clustering. To address this issue, we propose a deep embedding clustering algorithm driven by sample stability (DECS), which eliminates the requirement of pseudo targets. Specifically, we start by constructing the initial feature space with an autoencoder and then learn the cluster-oriented embedding feature constrained by sample stability. The sample stability aims to explore the deterministic relationship between samples and all cluster centroids, pulling samples to their respective clusters and keeping them away from other clusters with high determinacy. We analyzed the convergence of the loss using Lipschitz continuity in theory, which verifies the validity of the model. The experimental results on five datasets illustrate that the proposed method achieves superior performance compared to state-of-the-art clustering approaches.