Bridging Gaps: Federated Multi-View Clustering in Heterogeneous Hybrid Views

Recently, federated multi-view clustering (FedMVC) has emerged to explore cluster structures in multi-view data distributed on multiple clients. Existing approaches often assume that clients are isomorphic and all of them belong to either single-view clients or multi-view clients. Despite their success, these methods also present limitations when dealing with practical FedMVC scenarios involving heterogeneous hybrid views, where a mixture of both single-view and multi-view clients exhibit varying degrees of heterogeneity. In this paper, we propose a novel FedMVC framework, which concurrently addresses two challenges associated with heterogeneous hybrid views, i.e., client gap and view gap. To address the client gap, we design a local-synergistic contrastive learning approach that helps single-view clients and multi-view clients achieve consistency for mitigating heterogeneity among all clients. To address the view gap, we develop a global-specific weighting aggregation method, which encourages global models to learn complementary features from hybrid views. The interplay between local-synergistic contrastive learning and global-specific weighting aggregation mutually enhances the exploration of the data cluster structures distributed on multiple clients. Theoretical analysis and extensive experiments demonstrate that our method can handle the heterogeneous hybrid views in FedMVC and outperforms state-of-the-art methods. The code is available at \url{https://github.com/5Martina5/FMCSC}.

Contrastive Multi-view Hyperbolic Hierarchical Clustering

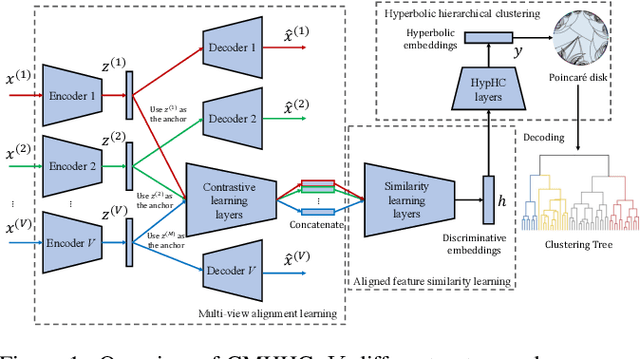
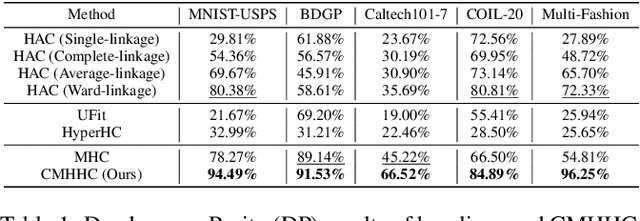
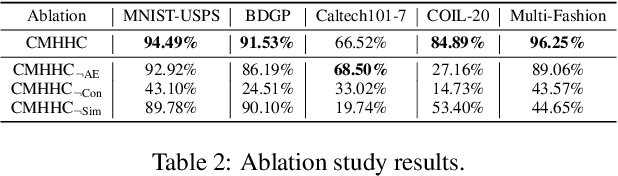
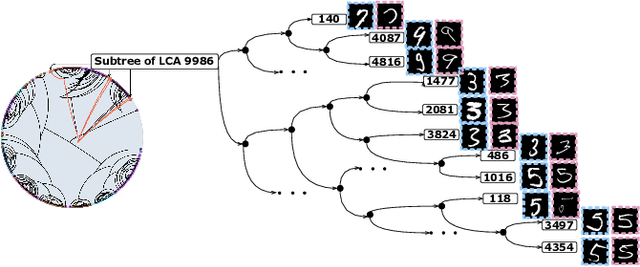
Hierarchical clustering recursively partitions data at an increasingly finer granularity. In real-world applications, multi-view data have become increasingly important. This raises a less investigated problem, i.e., multi-view hierarchical clustering, to better understand the hierarchical structure of multi-view data. To this end, we propose a novel neural network-based model, namely Contrastive Multi-view Hyperbolic Hierarchical Clustering (CMHHC). It consists of three components, i.e., multi-view alignment learning, aligned feature similarity learning, and continuous hyperbolic hierarchical clustering. First, we align sample-level representations across multiple views in a contrastive way to capture the view-invariance information. Next, we utilize both the manifold and Euclidean similarities to improve the metric property. Then, we embed the representations into a hyperbolic space and optimize the hyperbolic embeddings via a continuous relaxation of hierarchical clustering loss. Finally, a binary clustering tree is decoded from optimized hyperbolic embeddings. Experimental results on five real-world datasets demonstrate the effectiveness of the proposed method and its components.