Algorithmic Robust Forecast Aggregation

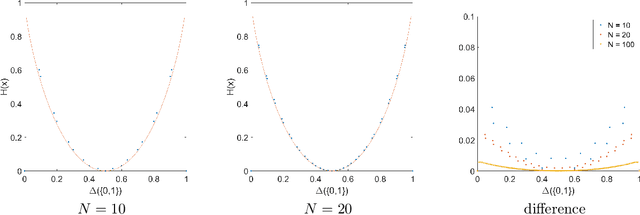
Forecast aggregation combines the predictions of multiple forecasters to improve accuracy. However, the lack of knowledge about forecasters' information structure hinders optimal aggregation. Given a family of information structures, robust forecast aggregation aims to find the aggregator with minimal worst-case regret compared to the omniscient aggregator. Previous approaches for robust forecast aggregation rely on heuristic observations and parameter tuning. We propose an algorithmic framework for robust forecast aggregation. Our framework provides efficient approximation schemes for general information aggregation with a finite family of possible information structures. In the setting considered by Arieli et al. (2018) where two agents receive independent signals conditioned on a binary state, our framework also provides efficient approximation schemes by imposing Lipschitz conditions on the aggregator or discrete conditions on agents' reports. Numerical experiments demonstrate the effectiveness of our method by providing a nearly optimal aggregator in the setting considered by Arieli et al. (2018).

Multi-agent Performative Prediction: From Global Stability and Optimality to Chaos

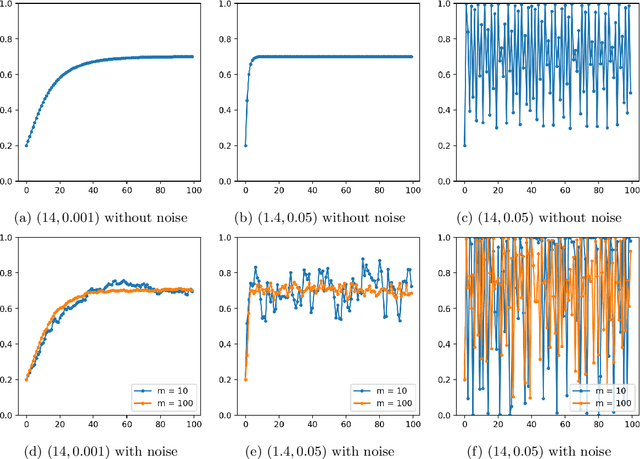
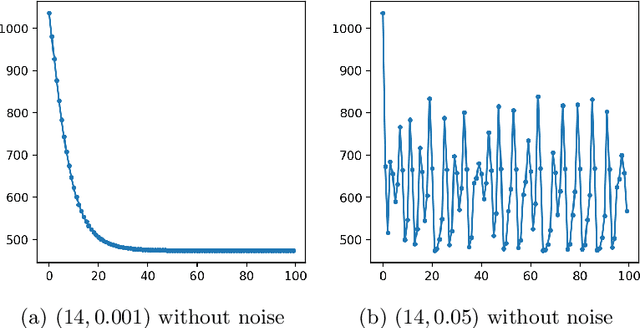
The recent framework of performative prediction is aimed at capturing settings where predictions influence the target/outcome they want to predict. In this paper, we introduce a natural multi-agent version of this framework, where multiple decision makers try to predict the same outcome. We showcase that such competition can result in interesting phenomena by proving the possibility of phase transitions from stability to instability and eventually chaos. Specifically, we present settings of multi-agent performative prediction where under sufficient conditions their dynamics lead to global stability and optimality. In the opposite direction, when the agents are not sufficiently cautious in their learning/updates rates, we show that instability and in fact formal chaos is possible. We complement our theoretical predictions with simulations showcasing the predictive power of our results.

Optimal Scoring Rule Design

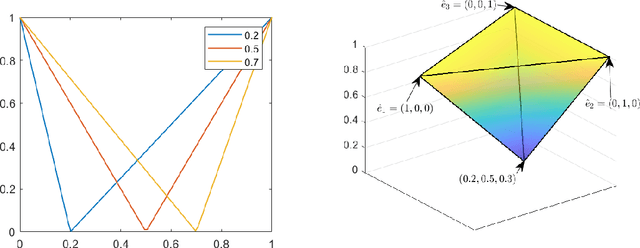
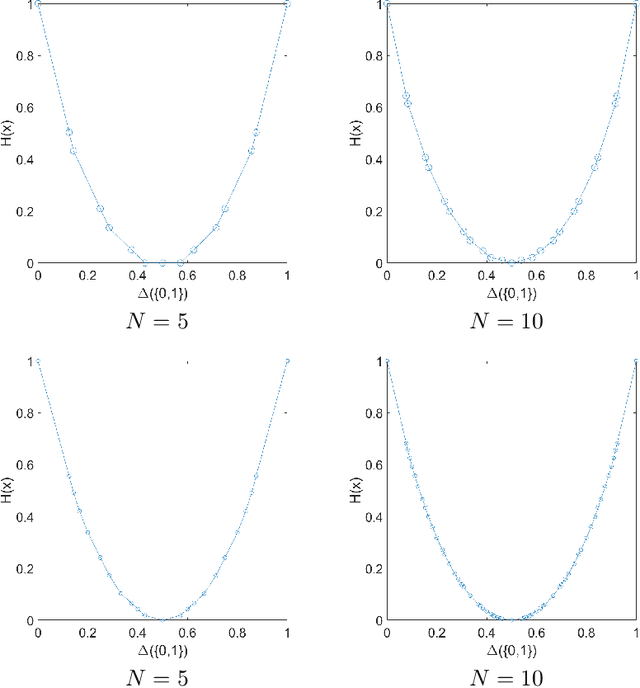
This paper introduces an optimization problem for proper scoring rule design. Consider a principal who wants to collect an agent's prediction about an unknown state. The agent can either report his prior prediction or access a costly signal and report the posterior prediction. Given a collection of possible distributions containing the agent's posterior prediction distribution, the principal's objective is to design a bounded scoring rule to maximize the agent's worst-case payoff increment between reporting his posterior prediction and reporting his prior prediction. We study two settings of such optimization for proper scoring rules: static and asymptotic settings. In the static setting, where the agent can access one signal, we propose an efficient algorithm to compute an optimal scoring rule when the collection of distributions is finite. The agent can adaptively and indefinitely refine his prediction in the asymptotic setting. We first consider a sequence of collections of posterior distributions with vanishing covariance, which emulates general estimators with large samples, and show the optimality of the quadratic scoring rule. Then, when the agent's posterior distribution is a Beta-Bernoulli process, we find that the log scoring rule is optimal. We also prove the optimality of the log scoring rule over a smaller set of functions for categorical distributions with Dirichlet priors.

Learning and Strongly Truthful Multi-Task Peer Prediction: A Variational Approach

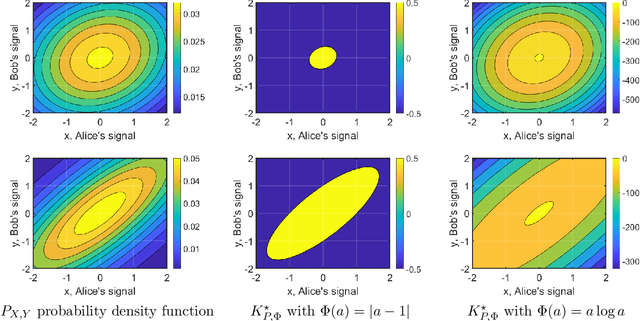
Peer prediction mechanisms incentivize agents to truthfully report their signals even in the absence of verification by comparing agents' reports with those of their peers. In the detail-free multi-task setting, agents respond to multiple independent and identically distributed tasks, and the mechanism does not know the prior distribution of agents' signals. The goal is to provide an $\epsilon$-strongly truthful mechanism where truth-telling rewards agents "strictly" more than any other strategy profile (with $\epsilon$ additive error), and to do so while requiring as few tasks as possible. We design a family of mechanisms with a scoring function that maps a pair of reports to a score. The mechanism is strongly truthful if the scoring function is "prior ideal," and $\epsilon$-strongly truthful as long as the scoring function is sufficiently close to the ideal one. This reduces the above mechanism design problem to a learning problem -- specifically learning an ideal scoring function. We leverage this reduction to obtain the following three results. 1) We show how to derive good bounds on the number of tasks required for different types of priors. Our reduction applies to myriad continuous signal space settings. This is the first peer-prediction mechanism on continuous signals designed for the multi-task setting. 2) We show how to turn a soft-predictor of an agent's signals (given the other agents' signals) into a mechanism. This allows the practical use of machine learning algorithms that give good results even when many agents provide noisy information. 3) For finite signal spaces, we obtain $\epsilon$-strongly truthful mechanisms on any stochastically relevant prior, which is the maximal possible prior. In contrast, prior work only achieves a weaker notion of truthfulness (informed truthfulness) or requires stronger assumptions on the prior.