Adversarial Generation and Collaborative Evolution of Safety-Critical Scenarios for Autonomous Vehicles

The generation of safety-critical scenarios in simulation has become increasingly crucial for safety evaluation in autonomous vehicles prior to road deployment in society. However, current approaches largely rely on predefined threat patterns or rule-based strategies, which limit their ability to expose diverse and unforeseen failure modes. To overcome these, we propose ScenGE, a framework that can generate plentiful safety-critical scenarios by reasoning novel adversarial cases and then amplifying them with complex traffic flows. Given a simple prompt of a benign scene, it first performs Meta-Scenario Generation, where a large language model, grounded in structured driving knowledge, infers an adversarial agent whose behavior poses a threat that is both plausible and deliberately challenging. This meta-scenario is then specified in executable code for precise in-simulator control. Subsequently, Complex Scenario Evolution uses background vehicles to amplify the core threat introduced by Meta-Scenario. It builds an adversarial collaborator graph to identify key agent trajectories for optimization. These perturbations are designed to simultaneously reduce the ego vehicle's maneuvering space and create critical occlusions. Extensive experiments conducted on multiple reinforcement learning based AV models show that ScenGE uncovers more severe collision cases (+31.96%) on average than SoTA baselines. Additionally, our ScenGE can be applied to large model based AV systems and deployed on different simulators; we further observe that adversarial training on our scenarios improves the model robustness. Finally, we validate our framework through real-world vehicle tests and human evaluation, confirming that the generated scenarios are both plausible and critical. We hope our paper can build up a critical step towards building public trust and ensuring their safe deployment.

Mitigating the Participation Bias by Balancing Extreme Ratings

Rating aggregation plays a crucial role in various fields, such as product recommendations, hotel rankings, and teaching evaluations. However, traditional averaging methods can be affected by participation bias, where some raters do not participate in the rating process, leading to potential distortions. In this paper, we consider a robust rating aggregation task under the participation bias. We assume that raters may not reveal their ratings with a certain probability depending on their individual ratings, resulting in partially observed samples. Our goal is to minimize the expected squared loss between the aggregated ratings and the average of all underlying ratings (possibly unobserved) in the worst-case scenario. We focus on two settings based on whether the sample size (i.e. the number of raters) is known. In the first setting, where the sample size is known, we propose an aggregator, named as the Balanced Extremes Aggregator. It estimates unrevealed ratings with a balanced combination of extreme ratings. When the sample size is unknown, we derive another aggregator, the Polarizing-Averaging Aggregator, which becomes optimal as the sample size grows to infinity. Numerical results demonstrate the superiority of our proposed aggregators in mitigating participation bias, compared to simple averaging and the spectral method. Furthermore, we validate the effectiveness of our aggregators on a real-world dataset.

Robust Decision Aggregation with Adversarial Experts

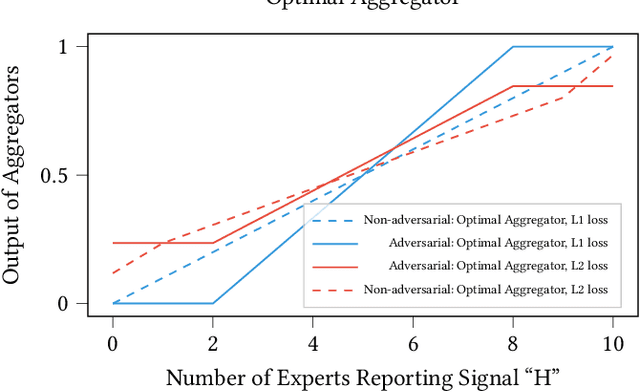
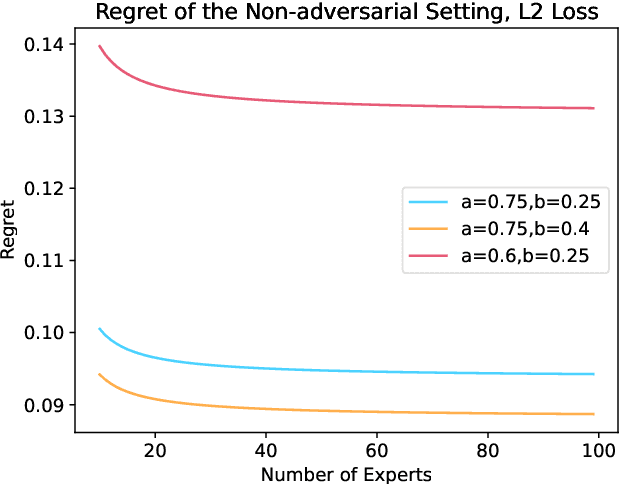
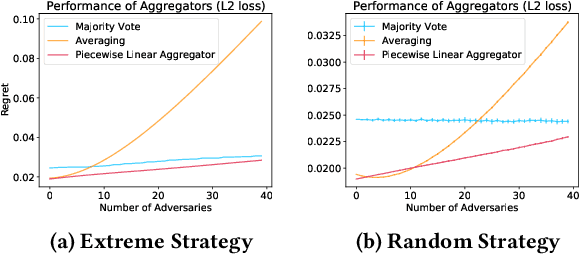
We consider a binary decision aggregation problem in the presence of both truthful and adversarial experts. The truthful experts will report their private signals truthfully with proper incentive, while the adversarial experts can report arbitrarily. The decision maker needs to design a robust aggregator to forecast the true state of the world based on the reports of experts. The decision maker does not know the specific information structure, which is a joint distribution of signals, states, and strategies of adversarial experts. We want to find the optimal aggregator minimizing regret under the worst information structure. The regret is defined by the difference in expected loss between the aggregator and a benchmark who makes the optimal decision given the joint distribution and reports of truthful experts. We prove that when the truthful experts are symmetric and adversarial experts are not too numerous, the truncated mean is optimal, which means that we remove some lowest reports and highest reports and take averaging among the left reports. Moreover, for many settings, the optimal aggregators are in the family of piecewise linear functions. The regret is independent of the total number of experts but only depends on the ratio of adversaries. We evaluate our aggregators by numerical experiment in an ensemble learning task. We also obtain some negative results for the aggregation problem with adversarial experts under some more general information structures and experts' report space.

Algorithmic Robust Forecast Aggregation

Forecast aggregation combines the predictions of multiple forecasters to improve accuracy. However, the lack of knowledge about forecasters' information structure hinders optimal aggregation. Given a family of information structures, robust forecast aggregation aims to find the aggregator with minimal worst-case regret compared to the omniscient aggregator. Previous approaches for robust forecast aggregation rely on heuristic observations and parameter tuning. We propose an algorithmic framework for robust forecast aggregation. Our framework provides efficient approximation schemes for general information aggregation with a finite family of possible information structures. In the setting considered by Arieli et al. (2018) where two agents receive independent signals conditioned on a binary state, our framework also provides efficient approximation schemes by imposing Lipschitz conditions on the aggregator or discrete conditions on agents' reports. Numerical experiments demonstrate the effectiveness of our method by providing a nearly optimal aggregator in the setting considered by Arieli et al. (2018).

Near-Optimal Experimental Design Under the Budget Constraint in Online Platforms

A/B testing, or controlled experiments, is the gold standard approach to causally compare the performance of algorithms on online platforms. However, conventional Bernoulli randomization in A/B testing faces many challenges such as spillover and carryover effects. Our study focuses on another challenge, especially for A/B testing on two-sided platforms -- budget constraints. Buyers on two-sided platforms often have limited budgets, where the conventional A/B testing may be infeasible to be applied, partly because two variants of allocation algorithms may conflict and lead some buyers to exceed their budgets if they are implemented simultaneously. We develop a model to describe two-sided platforms where buyers have limited budgets. We then provide an optimal experimental design that guarantees small bias and minimum variance. Bias is lower when there is more budget and a higher supply-demand rate. We test our experimental design on both synthetic data and real-world data, which verifies the theoretical results and shows our advantage compared to Bernoulli randomization.