Robust Decision Aggregation with Adversarial Experts
Paper and Code
Mar 13, 2024
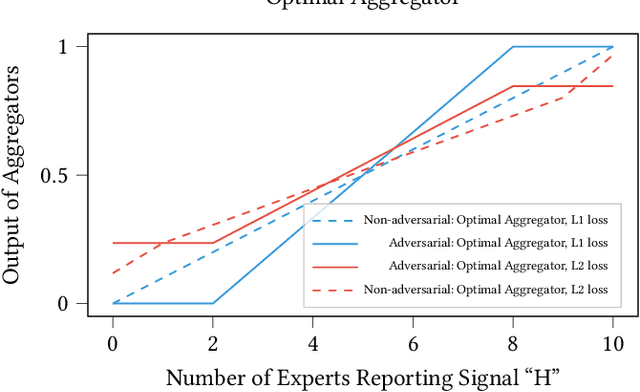
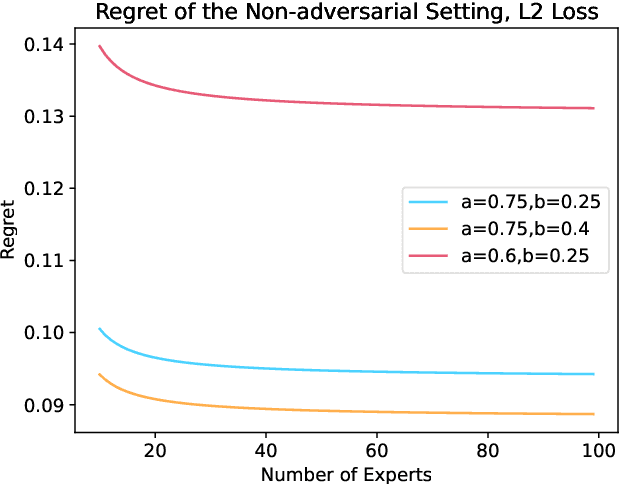
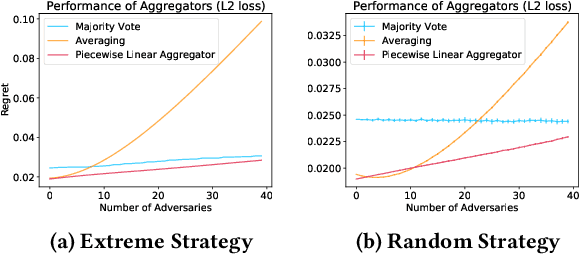
We consider a binary decision aggregation problem in the presence of both truthful and adversarial experts. The truthful experts will report their private signals truthfully with proper incentive, while the adversarial experts can report arbitrarily. The decision maker needs to design a robust aggregator to forecast the true state of the world based on the reports of experts. The decision maker does not know the specific information structure, which is a joint distribution of signals, states, and strategies of adversarial experts. We want to find the optimal aggregator minimizing regret under the worst information structure. The regret is defined by the difference in expected loss between the aggregator and a benchmark who makes the optimal decision given the joint distribution and reports of truthful experts. We prove that when the truthful experts are symmetric and adversarial experts are not too numerous, the truncated mean is optimal, which means that we remove some lowest reports and highest reports and take averaging among the left reports. Moreover, for many settings, the optimal aggregators are in the family of piecewise linear functions. The regret is independent of the total number of experts but only depends on the ratio of adversaries. We evaluate our aggregators by numerical experiment in an ensemble learning task. We also obtain some negative results for the aggregation problem with adversarial experts under some more general information structures and experts' report space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge