Fast and Optimal Laplacian Solver for Gradient-Domain Image Editing using Green Function Convolution

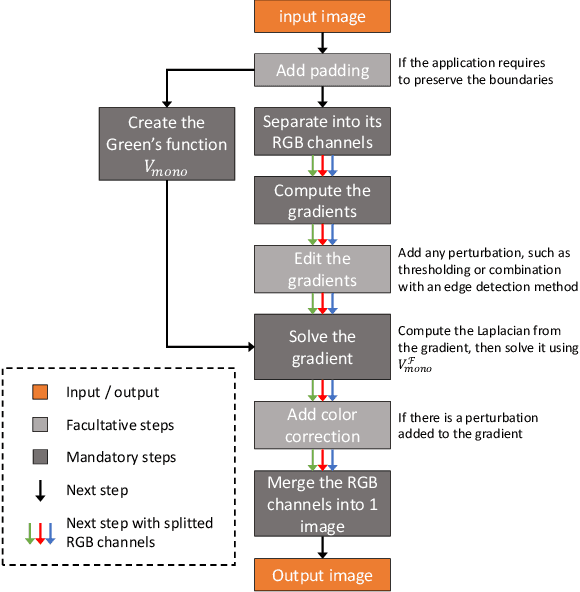
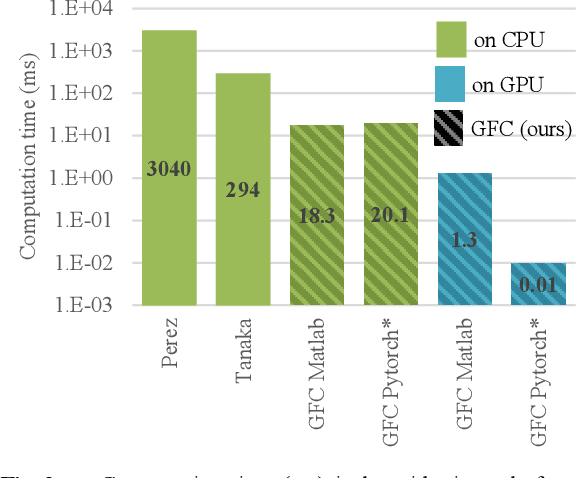
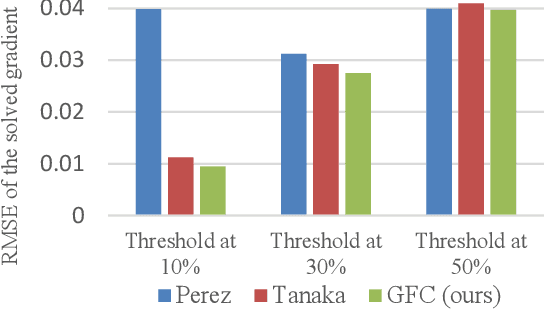
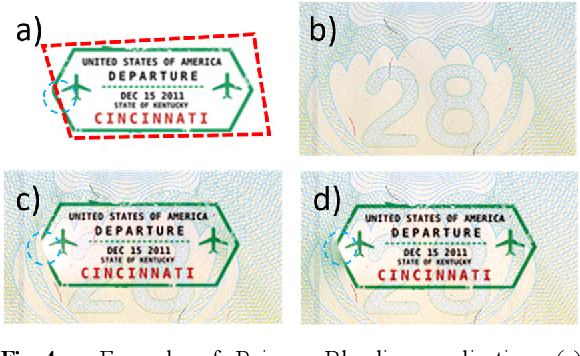
In computer vision, the gradient and Laplacian of an image are used in many different applications, such as edge detection, feature extraction and seamless image cloning. To obtain the gradient of an image, it requires the use of numerical derivatives, which are available in most computer vision toolboxes. However, the reverse problem is more difficult, since computing an image from its gradient requires to solve the Laplacian differential equation. The problem with the current existing methods is that they provide a solution that is prone to high numerical errors, and that they are either slow or require heavy parallel computing. The objective of this paper is to present a novel fast and robust method of computing the image from its gradient or Laplacian with minimal error, which can be used for gradient-domain editing. By using a single convolution based on Green's function, the whole process is faster and easier to implement. It can also be optimized on a GPU using fast Fourier transforms and can easily be generalized for an n-dimension image. The tests show that the gradient solver takes around 2 milliseconds (ms) to reconstruct an image of 801x1200 pixels compared to between 6ms and 3000ms for competing methods. Furthermore, it is proven mathematically that the proposed method gives the optimal result when a perturbation is added, meaning that it always produces the least-error solution for gradient-domain editing. Finally, the developed method is validated with examples of Poisson blending, gradient removal, edge preserving blurring and edge-preserving painting effect.

Computing the Spatial Probability of Inclusion inside Partial Contours for Computer Vision Applications

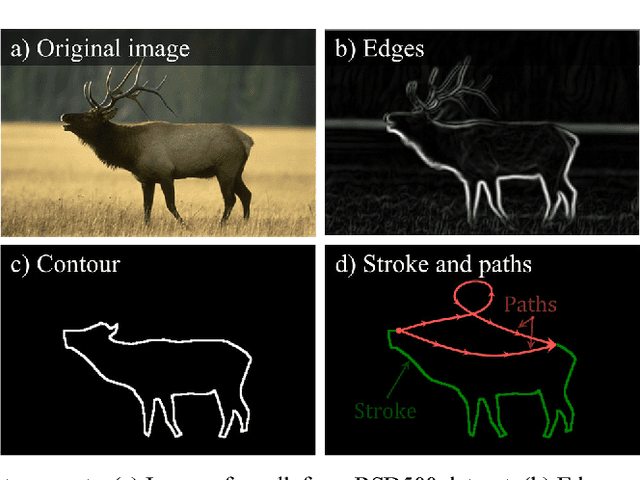
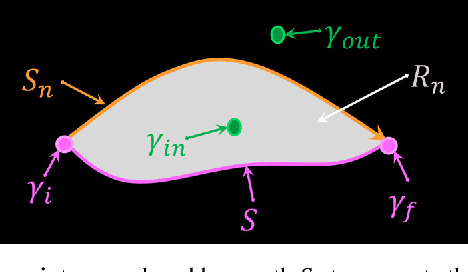
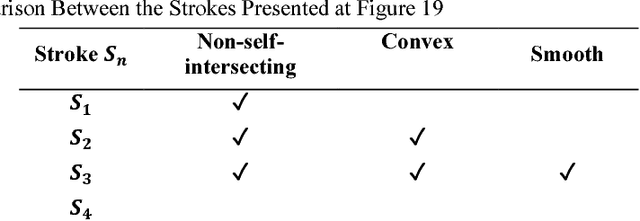
In Computer Vision, edge detection is one of the favored approaches for feature and object detection in images since it provides information about their objects boundaries. Other region-based approaches use probabilistic analysis such as clustering and Markov random fields, but those methods cannot be used to analyze edges and their interaction. In fact, only image segmentation can produce regions based on edges, but it requires thresholding by simply separating the regions into binary in-out information. Hence, there is currently a gap between edge-based and region-based algorithms, since edges cannot be used to study the properties of a region and vice versa. The objective of this paper is to present a novel spatial probability analysis that allows determining the probability of inclusion inside a set of partial contours (strokes). To answer this objective, we developed a new approach that uses electromagnetic convolutions and repulsion optimization to compute the required probabilities. Hence, it becomes possible to generate a continuous space of probability based only on the edge information, thus bridging the gap between the edge-based methods and the region-based methods. The developed method is consistent with the fundamental properties of inclusion probabilities and its results are validated by comparing an image with the probability-based estimation given by our algorithm. The method can also be generalized to take into consideration the intensity of the edges or to be used for 3D shapes. This is the first documented method that allows computing a space of probability based on interacting edges, which opens the path to broader applications such as image segmentation and contour completion.