Fast and Optimal Laplacian Solver for Gradient-Domain Image Editing using Green Function Convolution
Paper and Code
Feb 01, 2019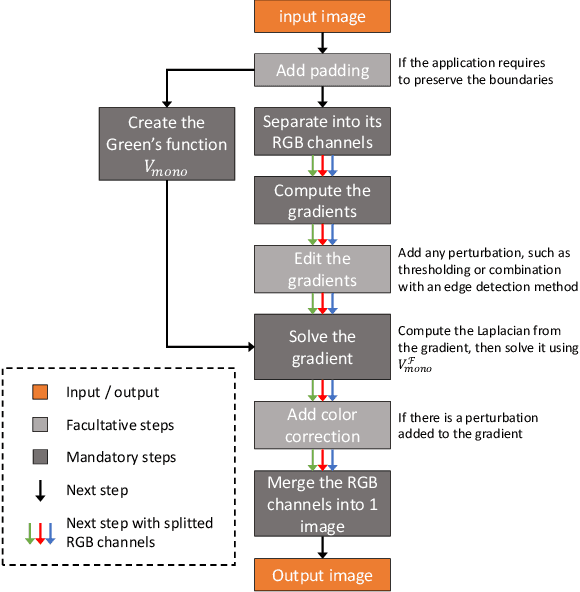
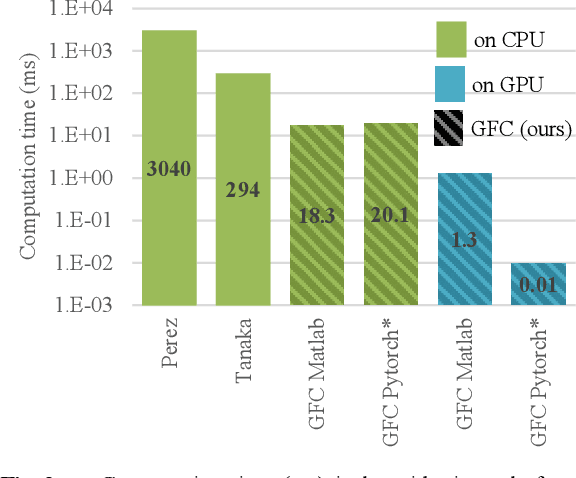
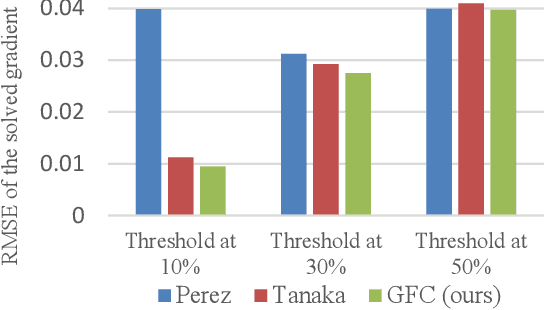
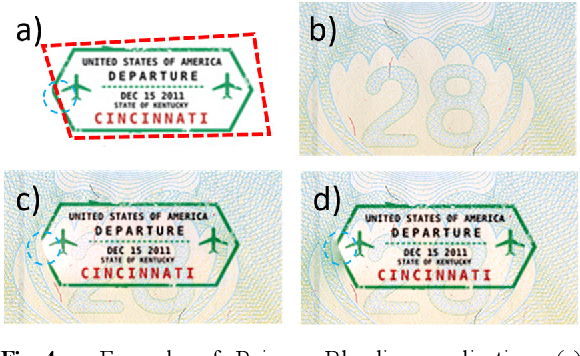
In computer vision, the gradient and Laplacian of an image are used in many different applications, such as edge detection, feature extraction and seamless image cloning. To obtain the gradient of an image, it requires the use of numerical derivatives, which are available in most computer vision toolboxes. However, the reverse problem is more difficult, since computing an image from its gradient requires to solve the Laplacian differential equation. The problem with the current existing methods is that they provide a solution that is prone to high numerical errors, and that they are either slow or require heavy parallel computing. The objective of this paper is to present a novel fast and robust method of computing the image from its gradient or Laplacian with minimal error, which can be used for gradient-domain editing. By using a single convolution based on Green's function, the whole process is faster and easier to implement. It can also be optimized on a GPU using fast Fourier transforms and can easily be generalized for an n-dimension image. The tests show that the gradient solver takes around 2 milliseconds (ms) to reconstruct an image of 801x1200 pixels compared to between 6ms and 3000ms for competing methods. Furthermore, it is proven mathematically that the proposed method gives the optimal result when a perturbation is added, meaning that it always produces the least-error solution for gradient-domain editing. Finally, the developed method is validated with examples of Poisson blending, gradient removal, edge preserving blurring and edge-preserving painting effect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge