Computing the Spatial Probability of Inclusion inside Partial Contours for Computer Vision Applications
Paper and Code
Jun 04, 2018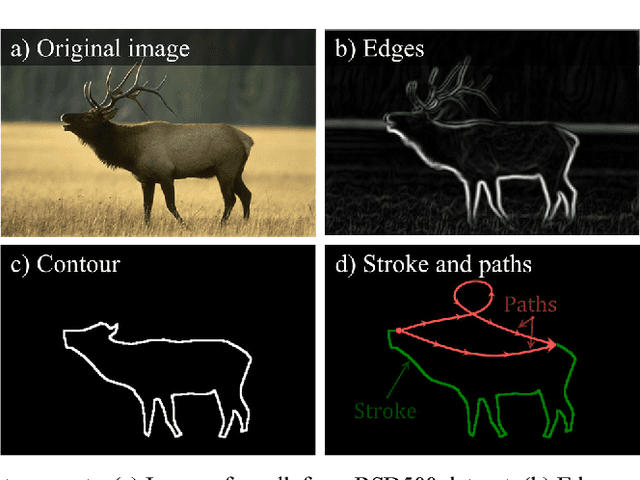

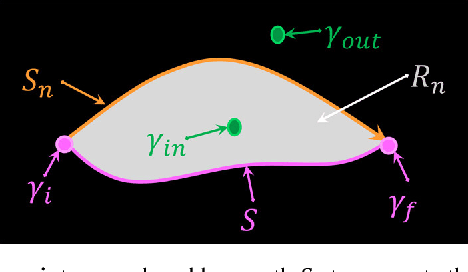
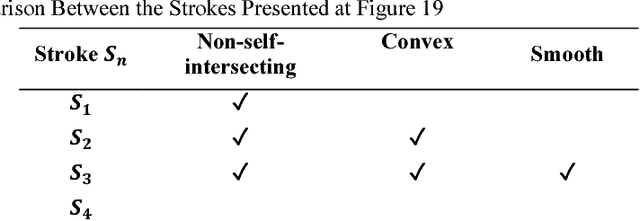
In Computer Vision, edge detection is one of the favored approaches for feature and object detection in images since it provides information about their objects boundaries. Other region-based approaches use probabilistic analysis such as clustering and Markov random fields, but those methods cannot be used to analyze edges and their interaction. In fact, only image segmentation can produce regions based on edges, but it requires thresholding by simply separating the regions into binary in-out information. Hence, there is currently a gap between edge-based and region-based algorithms, since edges cannot be used to study the properties of a region and vice versa. The objective of this paper is to present a novel spatial probability analysis that allows determining the probability of inclusion inside a set of partial contours (strokes). To answer this objective, we developed a new approach that uses electromagnetic convolutions and repulsion optimization to compute the required probabilities. Hence, it becomes possible to generate a continuous space of probability based only on the edge information, thus bridging the gap between the edge-based methods and the region-based methods. The developed method is consistent with the fundamental properties of inclusion probabilities and its results are validated by comparing an image with the probability-based estimation given by our algorithm. The method can also be generalized to take into consideration the intensity of the edges or to be used for 3D shapes. This is the first documented method that allows computing a space of probability based on interacting edges, which opens the path to broader applications such as image segmentation and contour completion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge