Fabio Sigrist
Selecting Hyperparameters for Tree-Boosting
Feb 05, 2026Abstract:Tree-boosting is a widely used machine learning technique for tabular data. However, its out-of-sample accuracy is critically dependent on multiple hyperparameters. In this article, we empirically compare several popular methods for hyperparameter optimization for tree-boosting including random grid search, the tree-structured Parzen estimator (TPE), Gaussian-process-based Bayesian optimization (GP-BO), Hyperband, the sequential model-based algorithm configuration (SMAC) method, and deterministic full grid search using $59$ regression and classification data sets. We find that the SMAC method clearly outperforms all the other considered methods. We further observe that (i) a relatively large number of trials larger than $100$ is required for accurate tuning, (ii) using default values for hyperparameters yields very inaccurate models, (iii) all considered hyperparameters can have a material effect on the accuracy of tree-boosting, i.e., there is no small set of hyperparameters that is more important than others, and (iv) choosing the number of boosting iterations using early stopping yields more accurate results compared to including it in the search space for regression tasks.
Scalable Computations for Generalized Mixed Effects Models with Crossed Random Effects Using Krylov Subspace Methods
May 14, 2025
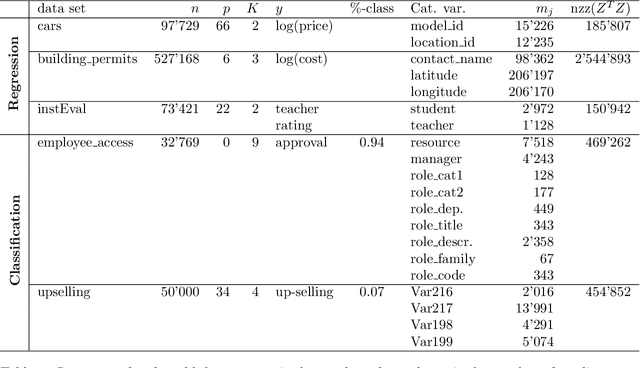
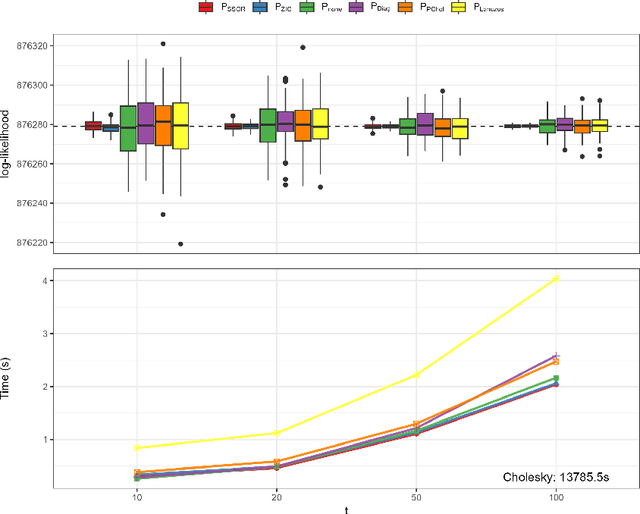
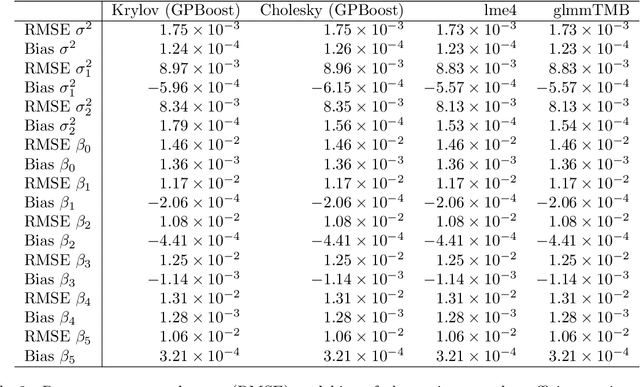
Abstract:Mixed effects models are widely used for modeling data with hierarchically grouped structures and high-cardinality categorical predictor variables. However, for high-dimensional crossed random effects, current standard computations relying on Cholesky decompositions can become prohibitively slow. In this work, we present novel Krylov subspace-based methods that address several existing computational bottlenecks. Among other things, we theoretically analyze and empirically evaluate various preconditioners for the conjugate gradient and stochastic Lanczos quadrature methods, derive new convergence results, and develop computationally efficient methods for calculating predictive variances. Extensive experiments using simulated and real-world data sets show that our proposed methods scale much better than Cholesky-based computations, for instance, achieving a runtime reduction of approximately two orders of magnitudes for both estimation and prediction. Moreover, our software implementation is up to 10'000 times faster and more stable than state-of-the-art implementations such as lme4 and glmmTMB when using default settings. Our methods are implemented in the free C++ software library GPBoost with high-level Python and R packages.
An accuracy-runtime trade-off comparison of scalable Gaussian process approximations for spatial data
Jan 20, 2025



Abstract:Gaussian processes (GPs) are flexible, probabilistic, non-parametric models widely employed in various fields such as spatial statistics, time series analysis, and machine learning. A drawback of Gaussian processes is their computational cost having $\mathcal{O}(N^3)$ time and $\mathcal{O}(N^2)$ memory complexity which makes them prohibitive for large datasets. Numerous approximation techniques have been proposed to address this limitation. In this work, we systematically compare the accuracy of different Gaussian process approximations concerning marginal likelihood evaluation, parameter estimation, and prediction taking into account the time required to achieve a certain accuracy. We analyze this trade-off between accuracy and runtime on multiple simulated and large-scale real-world datasets and find that Vecchia approximations consistently emerge as the most accurate in almost all experiments. However, for certain real-world data sets, low-rank inducing point-based methods, i.e., full-scale and modified predictive process approximations, can provide more accurate predictive distributions for extrapolation.
A Spatio-Temporal Machine Learning Model for Mortgage Credit Risk: Default Probabilities and Loan Portfolios
Oct 03, 2024Abstract:We introduce a novel machine learning model for credit risk by combining tree-boosting with a latent spatio-temporal Gaussian process model accounting for frailty correlation. This allows for modeling non-linearities and interactions among predictor variables in a flexible data-driven manner and for accounting for spatio-temporal variation that is not explained by observable predictor variables. We also show how estimation and prediction can be done in a computationally efficient manner. In an application to a large U.S. mortgage credit risk data set, we find that both predictive default probabilities for individual loans and predictive loan portfolio loss distributions obtained with our novel approach are more accurate compared to conventional independent linear hazard models and also linear spatio-temporal models. Using interpretability tools for machine learning models, we find that the likely reasons for this outperformance are strong interaction and non-linear effects in the predictor variables and the presence of large spatio-temporal frailty effects.
Iterative Methods for Full-Scale Gaussian Process Approximations for Large Spatial Data
May 23, 2024



Abstract:Gaussian processes are flexible probabilistic regression models which are widely used in statistics and machine learning. However, a drawback is their limited scalability to large data sets. To alleviate this, we consider full-scale approximations (FSAs) that combine predictive process methods and covariance tapering, thus approximating both global and local structures. We show how iterative methods can be used to reduce the computational costs for calculating likelihoods, gradients, and predictive distributions with FSAs. We introduce a novel preconditioner and show that it accelerates the conjugate gradient method's convergence speed and mitigates its sensitivity with respect to the FSA parameters and the eigenvalue structure of the original covariance matrix, and we demonstrate empirically that it outperforms a state-of-the-art pivoted Cholesky preconditioner. Further, we present a novel, accurate, and fast way to calculate predictive variances relying on stochastic estimations and iterative methods. In both simulated and real-world data experiments, we find that our proposed methodology achieves the same accuracy as Cholesky-based computations with a substantial reduction in computational time. Finally, we also compare different approaches for determining inducing points in predictive process and FSA models. All methods are implemented in a free C++ software library with high-level Python and R packages.
Iterative Methods for Vecchia-Laplace Approximations for Latent Gaussian Process Models
Oct 18, 2023Abstract:Latent Gaussian process (GP) models are flexible probabilistic non-parametric function models. Vecchia approximations are accurate approximations for GPs to overcome computational bottlenecks for large data, and the Laplace approximation is a fast method with asymptotic convergence guarantees to approximate marginal likelihoods and posterior predictive distributions for non-Gaussian likelihoods. Unfortunately, the computational complexity of combined Vecchia-Laplace approximations grows faster than linearly in the sample size when used in combination with direct solver methods such as the Cholesky decomposition. Computations with Vecchia-Laplace approximations thus become prohibitively slow precisely when the approximations are usually the most accurate, i.e., on large data sets. In this article, we present several iterative methods for inference with Vecchia-Laplace approximations which make computations considerably faster compared to Cholesky-based calculations. We analyze our proposed methods theoretically and in experiments with simulated and real-world data. In particular, we obtain a speed-up of an order of magnitude compared to Cholesky-based inference and a threefold increase in prediction accuracy in terms of the continuous ranked probability score compared to a state-of-the-art method on a large satellite data set. All methods are implemented in a free C++ software library with high-level Python and R packages.
A Comparison of Machine Learning Methods for Data with High-Cardinality Categorical Variables
Jul 05, 2023Abstract:High-cardinality categorical variables are variables for which the number of different levels is large relative to the sample size of a data set, or in other words, there are few data points per level. Machine learning methods can have difficulties with high-cardinality variables. In this article, we empirically compare several versions of two of the most successful machine learning methods, tree-boosting and deep neural networks, and linear mixed effects models using multiple tabular data sets with high-cardinality categorical variables. We find that, first, machine learning models with random effects have higher prediction accuracy than their classical counterparts without random effects, and, second, tree-boosting with random effects outperforms deep neural networks with random effects.
Latent Gaussian Model Boosting
May 21, 2021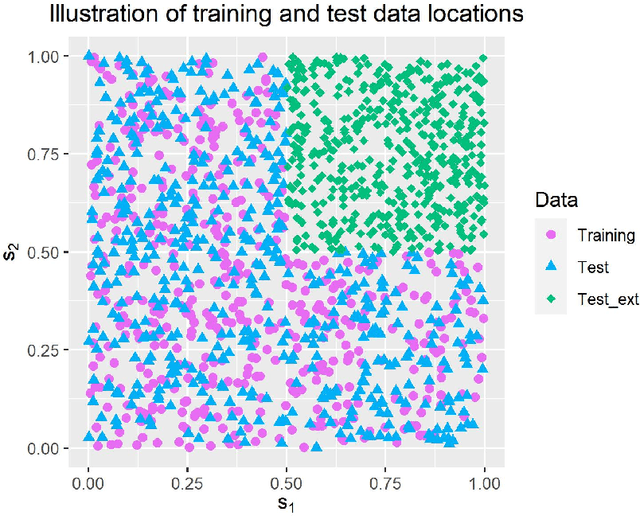
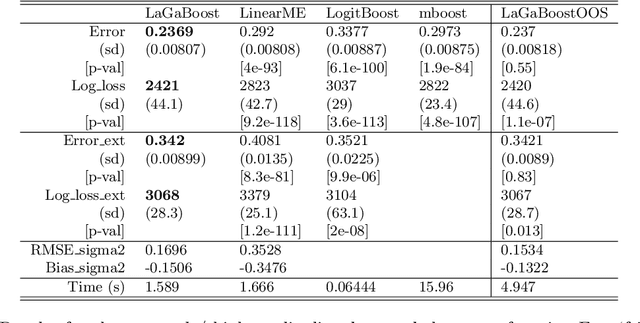
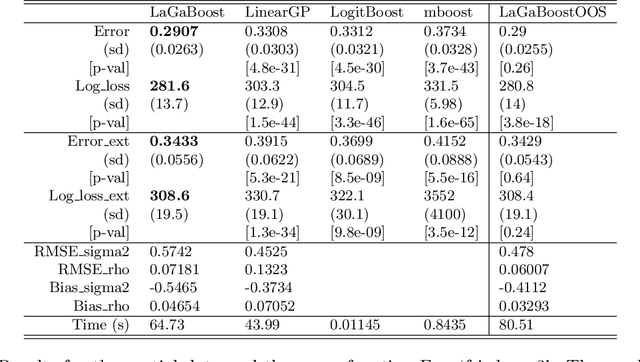
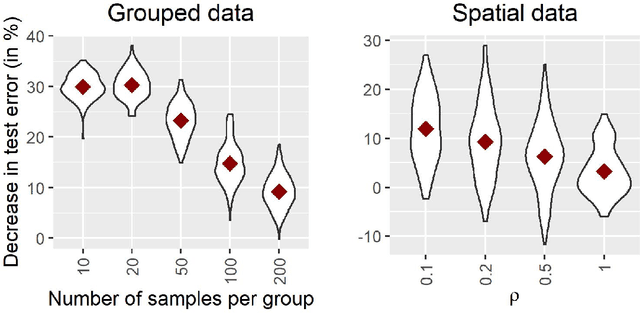
Abstract:Latent Gaussian models and boosting are widely used techniques in statistics and machine learning. Tree-boosting shows excellent predictive accuracy on many data sets, but potential drawbacks are that it assumes conditional independence of samples, produces discontinuous predictions for, e.g., spatial data, and it can have difficulty with high-cardinality categorical variables. Latent Gaussian models, such as Gaussian process and grouped random effects models, are flexible prior models that allow for making probabilistic predictions. However, existing latent Gaussian models usually assume either a zero or a linear prior mean function which can be an unrealistic assumption. This article introduces a novel approach that combines boosting and latent Gaussian models in order to remedy the above-mentioned drawbacks and to leverage the advantages of both techniques. We obtain increased predictive accuracy compared to existing approaches in both simulated and real-world data experiments.
Gaussian Process Boosting
Apr 06, 2020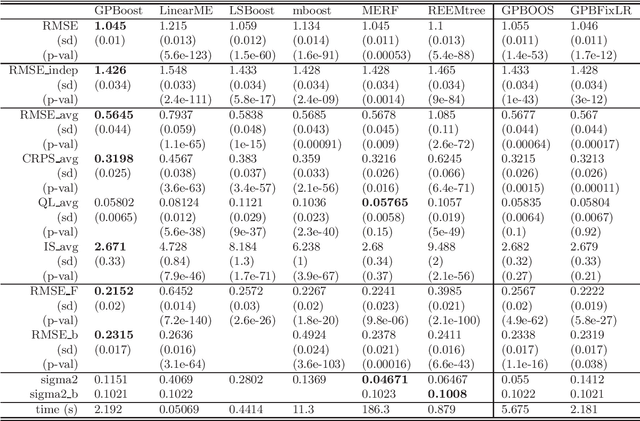
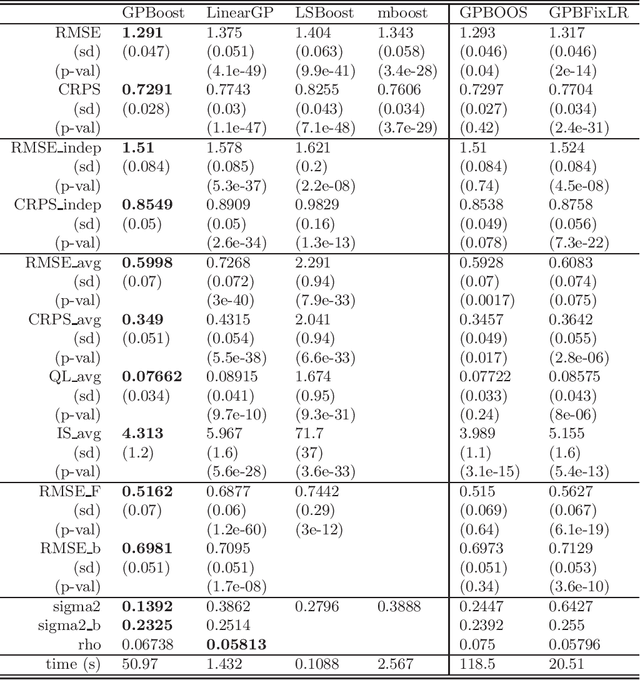
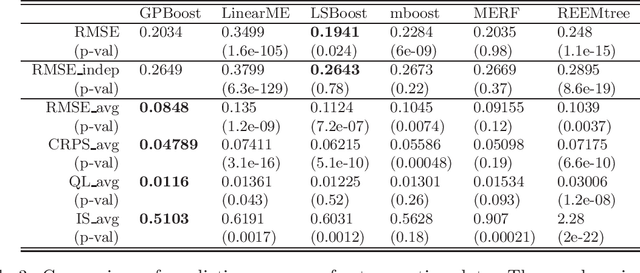
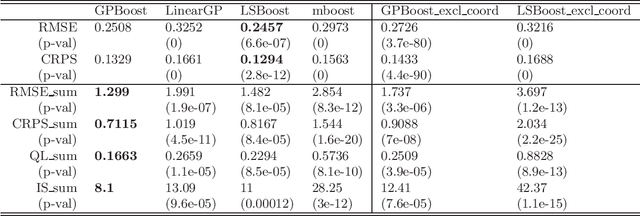
Abstract:In this article, we propose a novel way to combine boosting with Gaussian process and mixed effects models. This allows for relaxing (i) the linearity assumption for the mean function in Gaussian process and mixed effects models in a flexible non-parametric way and (ii) the independence assumption made in most boosting algorithms. The former is advantageous for predictive accuracy and for avoiding model misspecifications. The latter is important for more efficient learning of the mean function and for obtaining probabilistic predictions. In addition, we present an extension that scales to large data using a Vecchia approximation for the Gaussian process model relying on novel results for covariance parameter inference. We obtain increased predictive performance compared to existing approaches using several simulated datasets and in house price and online transaction applications.
KTBoost: Combined Kernel and Tree Boosting
Feb 11, 2019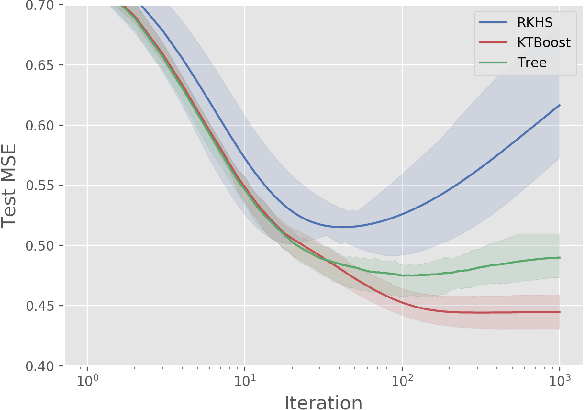
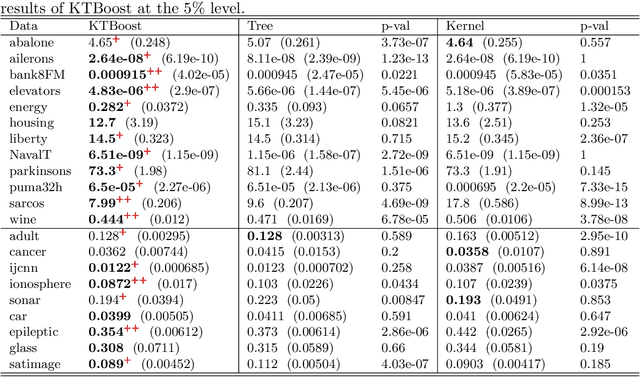
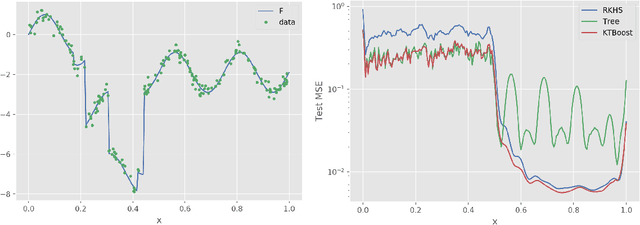
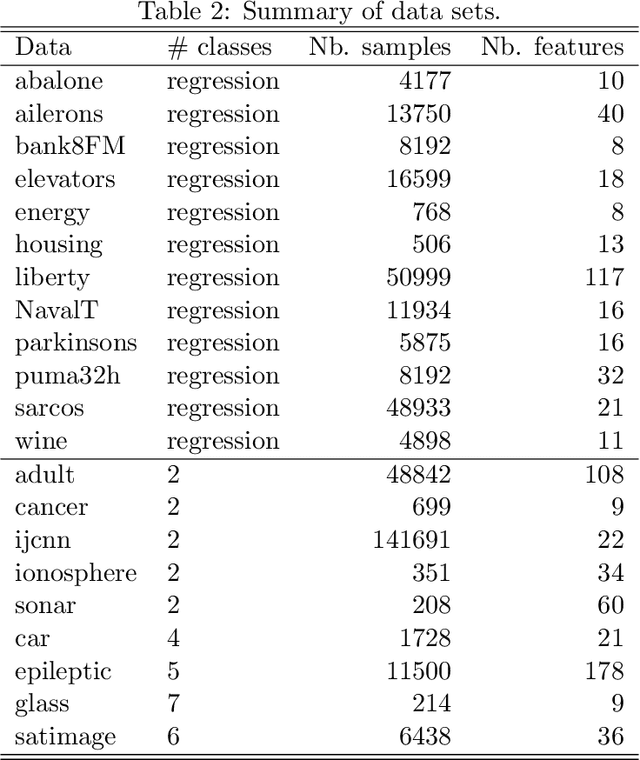
Abstract:In this article, we introduce a novel boosting algorithm called `KTBoost', which combines kernel boosting and tree boosting. In each boosting iteration, the algorithm adds either a regression tree or reproducing kernel Hilbert space (RKHS) regression function to the ensemble of base learners. Intuitively, the idea is that discontinuous trees and continuous RKHS regression functions complement each other, and that this combination allows for better learning of both continuous and discontinuous functions as well as functions that exhibit parts with varying degrees of regularity. We empirically show that KTBoost outperforms both tree and kernel boosting in terms of predictive accuracy on a wide array of data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge