Gaussian Process Boosting
Paper and Code
Apr 06, 2020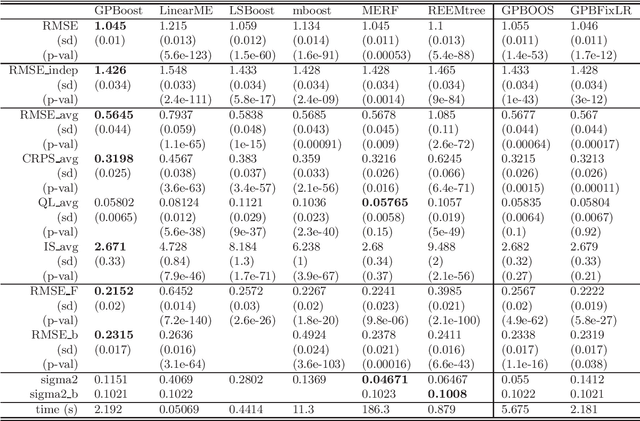
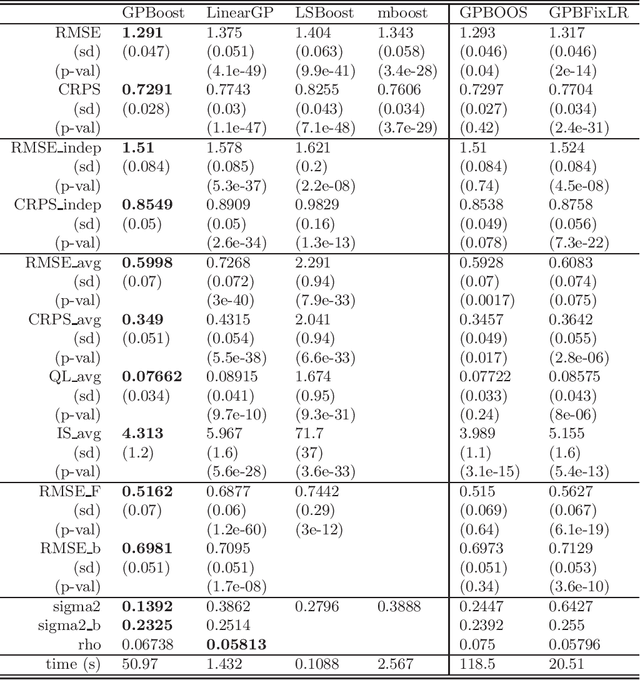
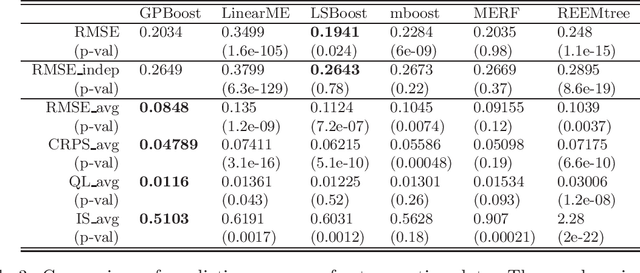
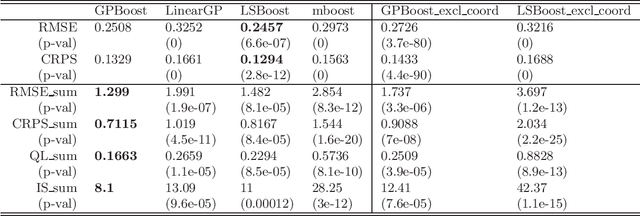
In this article, we propose a novel way to combine boosting with Gaussian process and mixed effects models. This allows for relaxing (i) the linearity assumption for the mean function in Gaussian process and mixed effects models in a flexible non-parametric way and (ii) the independence assumption made in most boosting algorithms. The former is advantageous for predictive accuracy and for avoiding model misspecifications. The latter is important for more efficient learning of the mean function and for obtaining probabilistic predictions. In addition, we present an extension that scales to large data using a Vecchia approximation for the Gaussian process model relying on novel results for covariance parameter inference. We obtain increased predictive performance compared to existing approaches using several simulated datasets and in house price and online transaction applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge