Latent Gaussian Model Boosting

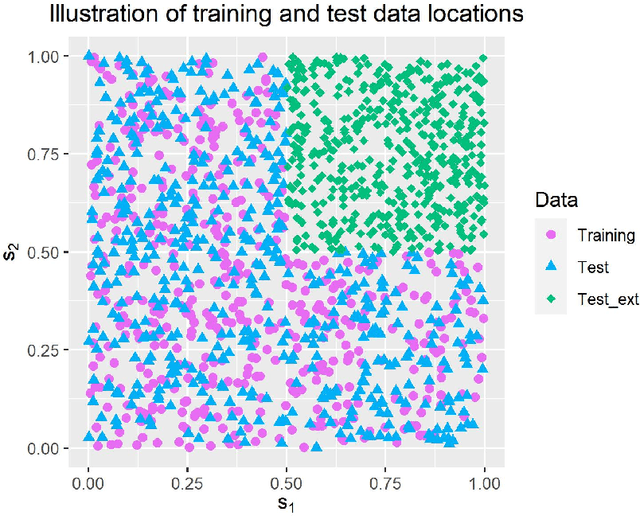
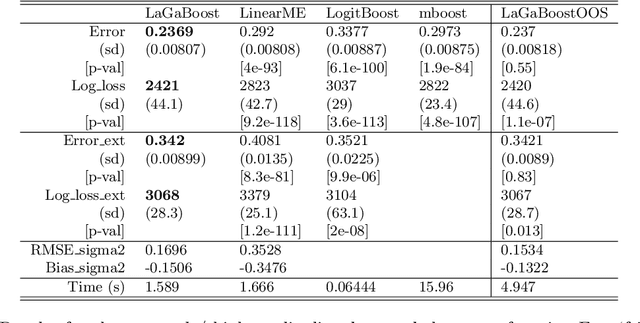
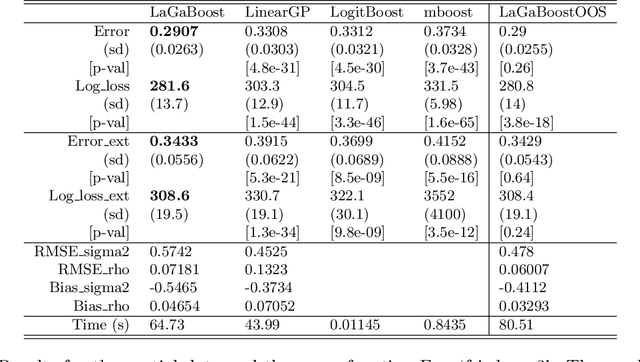
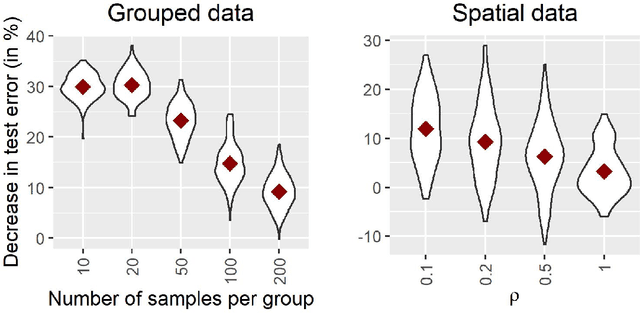
Latent Gaussian models and boosting are widely used techniques in statistics and machine learning. Tree-boosting shows excellent predictive accuracy on many data sets, but potential drawbacks are that it assumes conditional independence of samples, produces discontinuous predictions for, e.g., spatial data, and it can have difficulty with high-cardinality categorical variables. Latent Gaussian models, such as Gaussian process and grouped random effects models, are flexible prior models that allow for making probabilistic predictions. However, existing latent Gaussian models usually assume either a zero or a linear prior mean function which can be an unrealistic assumption. This article introduces a novel approach that combines boosting and latent Gaussian models in order to remedy the above-mentioned drawbacks and to leverage the advantages of both techniques. We obtain increased predictive accuracy compared to existing approaches in both simulated and real-world data experiments.