Ethan Jacob Moyer
EvoSTS Forecasting: Evolutionary Sparse Time-Series Forecasting
Apr 14, 2022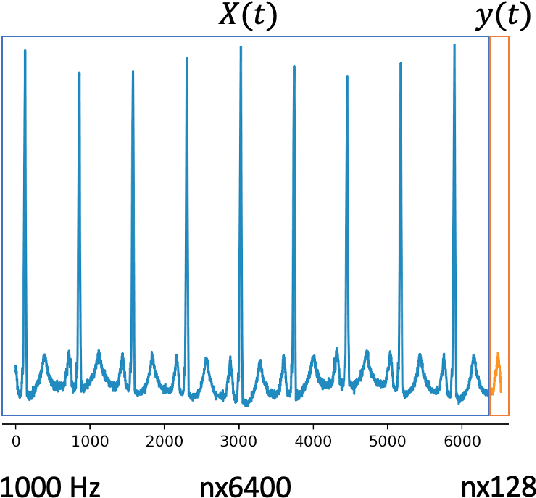
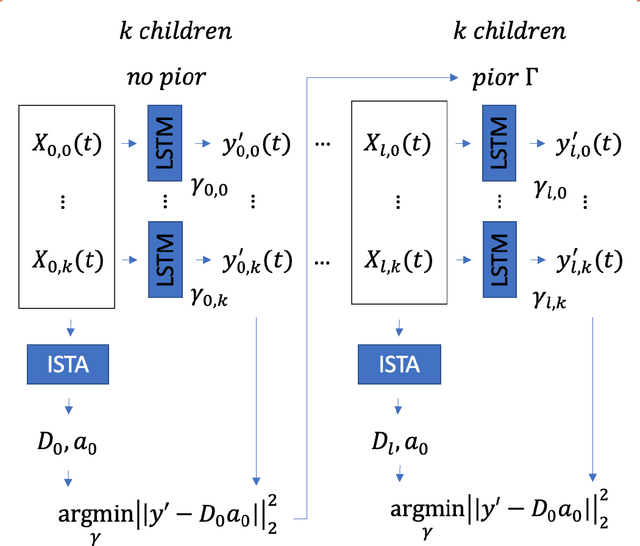

Abstract:In this work, we highlight our novel evolutionary sparse time-series forecasting algorithm also known as EvoSTS. The algorithm attempts to evolutionary prioritize weights of Long Short-Term Memory (LSTM) Network that best minimize the reconstruction loss of a predicted signal using a learned sparse coded dictionary. In each generation of our evolutionary algorithm, a set number of children with the same initial weights are spawned. Each child undergoes a training step and adjusts their weights on the same data. Due to stochastic back-propagation, the set of children has a variety of weights with different levels of performance. The weights that best minimize the reconstruction loss with a given signal dictionary are passed to the next generation. The predictions from the best-performing weights of the first and last generation are compared. We found improvements while comparing the weights of these two generations. However, due to several confounding parameters and hyperparameter limitations, some of the weights had negligible improvements. To the best of our knowledge, this is the first attempt to use sparse coding in this way to optimize time series forecasting model weights, such as those of an LSTM network.
Motif Identification using CNN-based Pairwise Subsequence Alignment Score Prediction
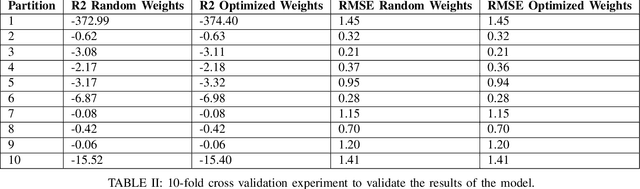
Jan 21, 2021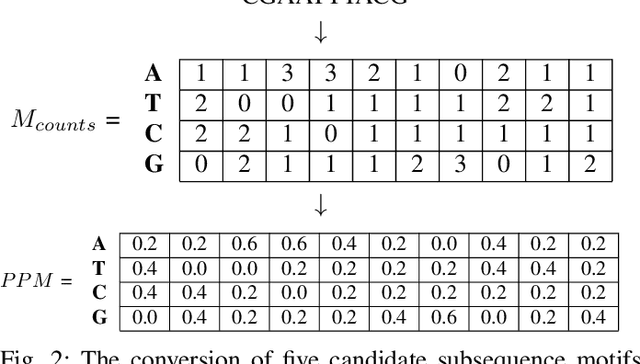

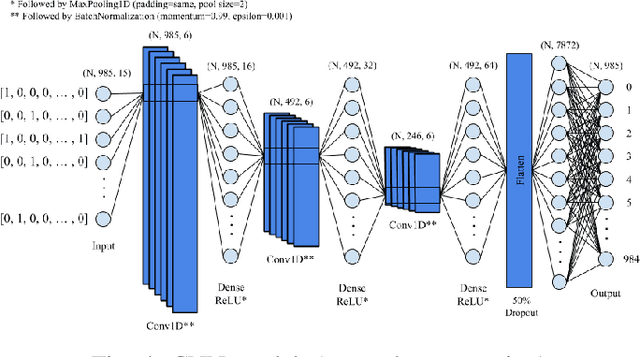

Abstract:A common problem in bioinformatics is related to identifying gene regulatory regions marked by relatively high frequencies of motifs, or deoxyribonucleic acid sequences that often code for transcription and enhancer proteins. Predicting alignment scores between subsequence k-mers and a given motif enables the identification of candidate regulatory regions in a gene, which correspond to the transcription of these proteins. We propose a one-dimensional (1-D) Convolution Neural Network trained on k-mer formatted sequences interspaced with the given motif pattern to predict pairwise alignment scores between the consensus motif and subsequence k-mers. Our model consists of fifteen layers with three rounds of a one-dimensional convolution layer, a batch normalization layer, a dense layer, and a 1-D maximum pooling layer. We train the model using mean squared error loss on four different data sets each with a different motif pattern randomly inserted in DNA sequences: the first three data sets have zero, one, and two mutations applied on each inserted motif, and the fourth data set represents the inserted motif as a position-specific probability matrix. We use a novel proposed metric in order to evaluate the model's performance, $S_{\alpha}$, which is based on the Jaccard Index. We use 10-fold cross validation to evaluate out model. Using $S_{\alpha}$, we measure the accuracy of the model by identifying the 15 highest-scoring 15-mer indices of the predicted scores that agree with that of the actual scores within a selected $\alpha$ region. For the best performing data set, our results indicate on average 99.3% of the top 15 motifs were identified correctly within a one base pair stride ($\alpha = 1$) in the out of sample data. To the best of our knowledge, this is a novel approach that illustrates how data formatted in an intelligent way can be extrapolated using machine learning.
Evaluating Online and Offline Accuracy Traversal Algorithms for k-Complete Neural Network Architectures
Jan 16, 2021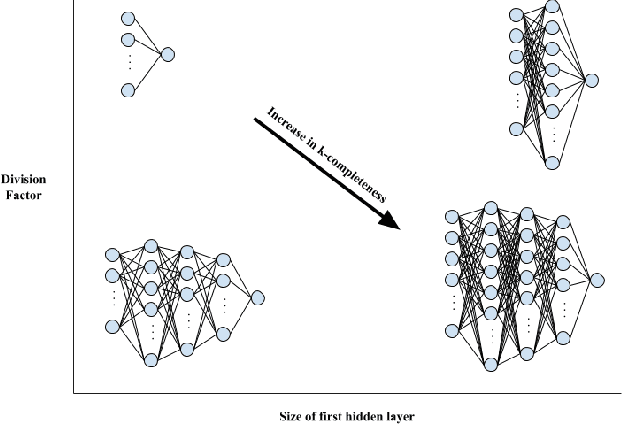
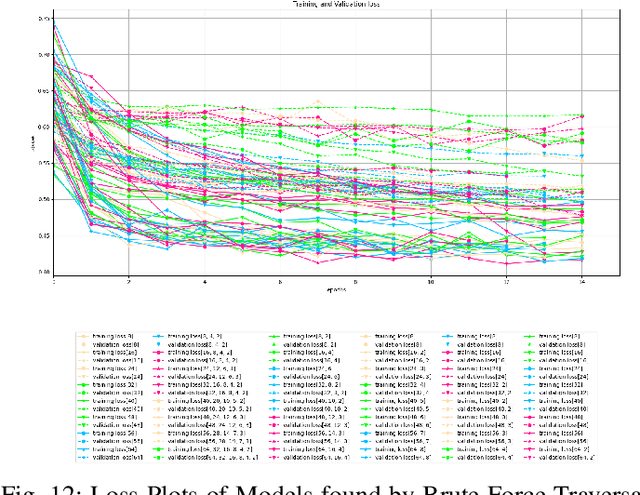
Abstract:Architecture sizes for neural networks have been studied widely and several search methods have been offered to find the best architecture size in the shortest amount of time possible. In this paper, we study compact neural network architectures for binary classification and investigate improvements in speed and accuracy when favoring overcomplete architecture candidates that have a very high-dimensional representation of the input. We hypothesize that an overcomplete model architecture that creates a relatively high-dimensional representation of the input will be not only be more accurate but would also be easier and faster to find. In an NxM search space, we propose an online traversal algorithm that finds the best architecture candidate in O(1) time for best case and O(N) amortized time for average case for any compact binary classification problem by using k-completeness as heuristics in our search. The two other offline search algorithms we implement are brute force traversal and diagonal traversal, which both find the best architecture candidate in O(NxM) time. We compare our new algorithm to brute force and diagonal searching as a baseline and report search time improvement of 52.1% over brute force and of 15.4% over diagonal search to find the most accurate neural network architecture when given the same dataset. In all cases discussed in the paper, our online traversal algorithm can find an accurate, if not better, architecture in significantly shorter amount of time.
Towards Searching Efficient and Accurate Neural Network Architectures in Binary Classification Problems
Jan 16, 2021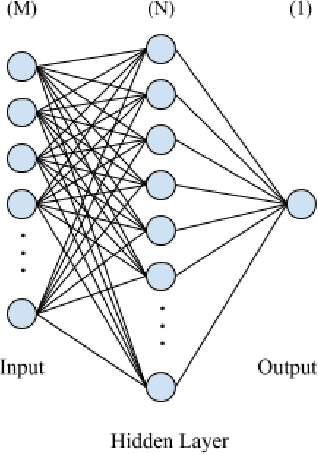
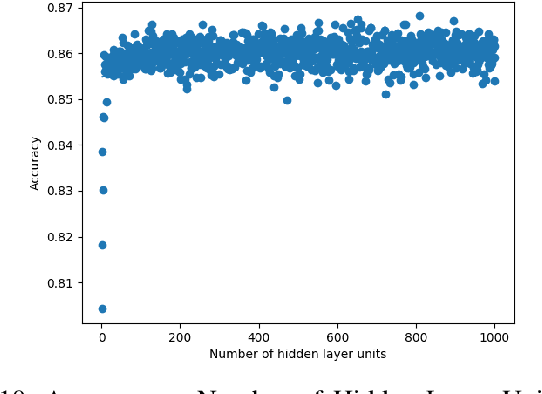
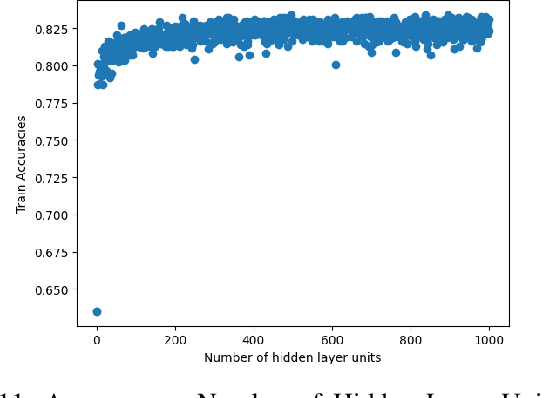
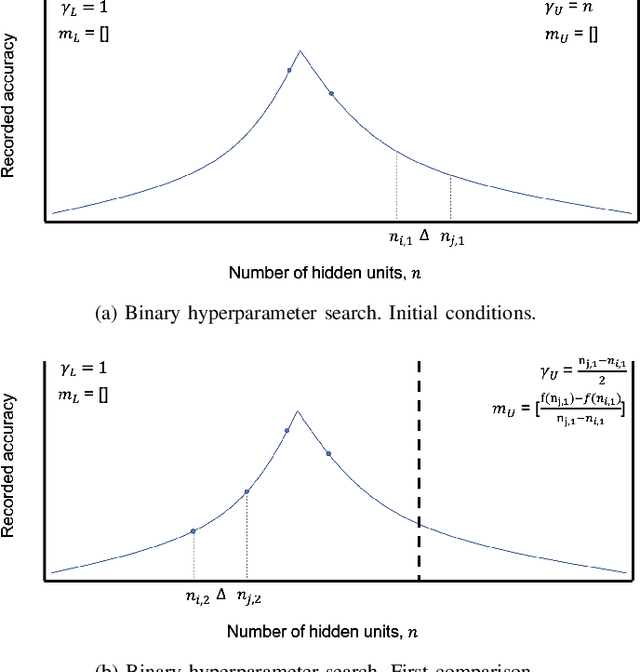
Abstract:In recent years, deep neural networks have had great success in machine learning and pattern recognition. Architecture size for a neural network contributes significantly to the success of any neural network. In this study, we optimize the selection process by investigating different search algorithms to find a neural network architecture size that yields the highest accuracy. We apply binary search on a very well-defined binary classification network search space and compare the results to those of linear search. We also propose how to relax some of the assumptions regarding the dataset so that our solution can be generalized to any binary classification problem. We report a 100-fold running time improvement over the naive linear search when we apply the binary search method to our datasets in order to find the best architecture candidate. By finding the optimal architecture size for any binary classification problem quickly, we hope that our research contributes to discovering intelligent algorithms for optimizing architecture size selection in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge