Motif Identification using CNN-based Pairwise Subsequence Alignment Score Prediction
Paper and Code
Jan 21, 2021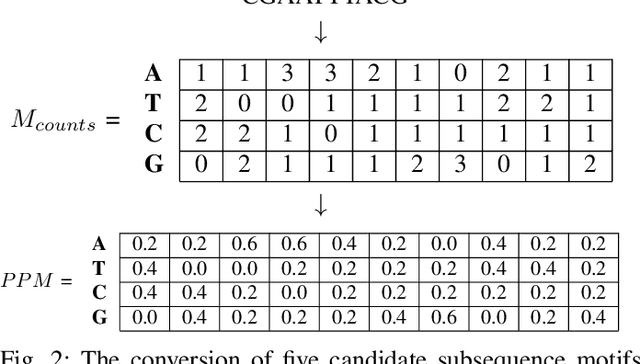

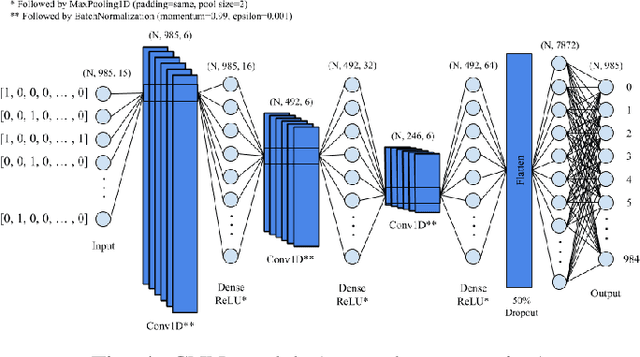

A common problem in bioinformatics is related to identifying gene regulatory regions marked by relatively high frequencies of motifs, or deoxyribonucleic acid sequences that often code for transcription and enhancer proteins. Predicting alignment scores between subsequence k-mers and a given motif enables the identification of candidate regulatory regions in a gene, which correspond to the transcription of these proteins. We propose a one-dimensional (1-D) Convolution Neural Network trained on k-mer formatted sequences interspaced with the given motif pattern to predict pairwise alignment scores between the consensus motif and subsequence k-mers. Our model consists of fifteen layers with three rounds of a one-dimensional convolution layer, a batch normalization layer, a dense layer, and a 1-D maximum pooling layer. We train the model using mean squared error loss on four different data sets each with a different motif pattern randomly inserted in DNA sequences: the first three data sets have zero, one, and two mutations applied on each inserted motif, and the fourth data set represents the inserted motif as a position-specific probability matrix. We use a novel proposed metric in order to evaluate the model's performance, $S_{\alpha}$, which is based on the Jaccard Index. We use 10-fold cross validation to evaluate out model. Using $S_{\alpha}$, we measure the accuracy of the model by identifying the 15 highest-scoring 15-mer indices of the predicted scores that agree with that of the actual scores within a selected $\alpha$ region. For the best performing data set, our results indicate on average 99.3% of the top 15 motifs were identified correctly within a one base pair stride ($\alpha = 1$) in the out of sample data. To the best of our knowledge, this is a novel approach that illustrates how data formatted in an intelligent way can be extrapolated using machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge