Evaluating Online and Offline Accuracy Traversal Algorithms for k-Complete Neural Network Architectures
Paper and Code
Jan 16, 2021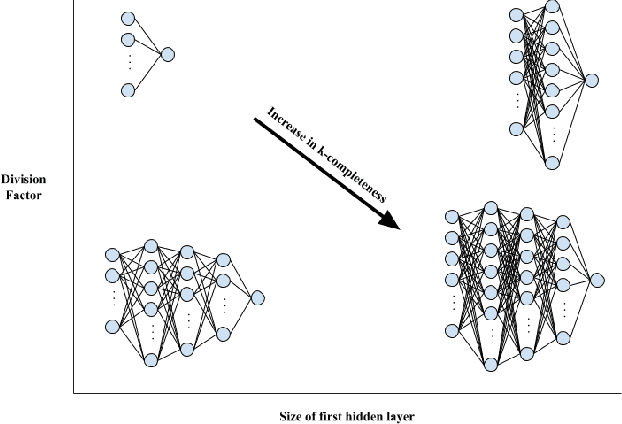
Architecture sizes for neural networks have been studied widely and several search methods have been offered to find the best architecture size in the shortest amount of time possible. In this paper, we study compact neural network architectures for binary classification and investigate improvements in speed and accuracy when favoring overcomplete architecture candidates that have a very high-dimensional representation of the input. We hypothesize that an overcomplete model architecture that creates a relatively high-dimensional representation of the input will be not only be more accurate but would also be easier and faster to find. In an NxM search space, we propose an online traversal algorithm that finds the best architecture candidate in O(1) time for best case and O(N) amortized time for average case for any compact binary classification problem by using k-completeness as heuristics in our search. The two other offline search algorithms we implement are brute force traversal and diagonal traversal, which both find the best architecture candidate in O(NxM) time. We compare our new algorithm to brute force and diagonal searching as a baseline and report search time improvement of 52.1% over brute force and of 15.4% over diagonal search to find the most accurate neural network architecture when given the same dataset. In all cases discussed in the paper, our online traversal algorithm can find an accurate, if not better, architecture in significantly shorter amount of time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge