Bootstrapping Expectiles in Reinforcement Learning

Many classic Reinforcement Learning (RL) algorithms rely on a Bellman operator, which involves an expectation over the next states, leading to the concept of bootstrapping. To introduce a form of pessimism, we propose to replace this expectation with an expectile. In practice, this can be very simply done by replacing the $L_2$ loss with a more general expectile loss for the critic. Introducing pessimism in RL is desirable for various reasons, such as tackling the overestimation problem (for which classic solutions are double Q-learning or the twin-critic approach of TD3) or robust RL (where transitions are adversarial). We study empirically these two cases. For the overestimation problem, we show that the proposed approach, ExpectRL, provides better results than a classic twin-critic. On robust RL benchmarks, involving changes of the environment, we show that our approach is more robust than classic RL algorithms. We also introduce a variation of ExpectRL combined with domain randomization which is competitive with state-of-the-art robust RL agents. Eventually, we also extend \ExpectRL with a mechanism for choosing automatically the expectile value, that is the degree of pessimism

Towards Minimax Optimality of Model-based Robust Reinforcement Learning

We study the sample complexity of obtaining an $\epsilon$-optimal policy in \emph{Robust} discounted Markov Decision Processes (RMDPs), given only access to a generative model of the nominal kernel. This problem is widely studied in the non-robust case, and it is known that any planning approach applied to an empirical MDP estimated with $\tilde{\mathcal{O}}(\frac{H^3 \mid S \mid\mid A \mid}{\epsilon^2})$ samples provides an $\epsilon$-optimal policy, which is minimax optimal. Results in the robust case are much more scarce. For $sa$- (resp $s$-)rectangular uncertainty sets, the best known sample complexity is $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid^2\mid A \mid}{\epsilon^2})$ (resp. $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid^2\mid A \mid^2}{\epsilon^2})$), for specific algorithms and when the uncertainty set is based on the total variation (TV), the KL or the Chi-square divergences. In this paper, we consider uncertainty sets defined with an $L_p$-ball (recovering the TV case), and study the sample complexity of \emph{any} planning algorithm (with high accuracy guarantee on the solution) applied to an empirical RMDP estimated using the generative model. In the general case, we prove a sample complexity of $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid\mid A \mid}{\epsilon^2})$ for both the $sa$- and $s$-rectangular cases (improvements of $\mid S \mid$ and $\mid S \mid\mid A \mid$ respectively). When the size of the uncertainty is small enough, we improve the sample complexity to $\tilde{\mathcal{O}}(\frac{H^3 \mid S \mid\mid A \mid }{\epsilon^2})$, recovering the lower-bound for the non-robust case for the first time and a robust lower-bound when the size of the uncertainty is small enough.

Robust Reinforcement Learning with Distributional Risk-averse formulation

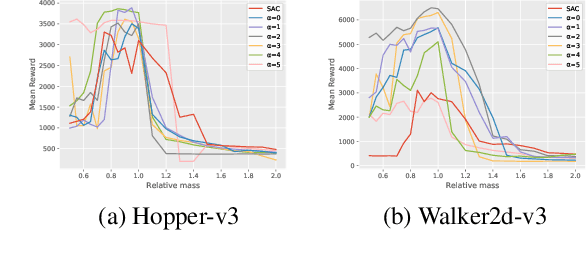
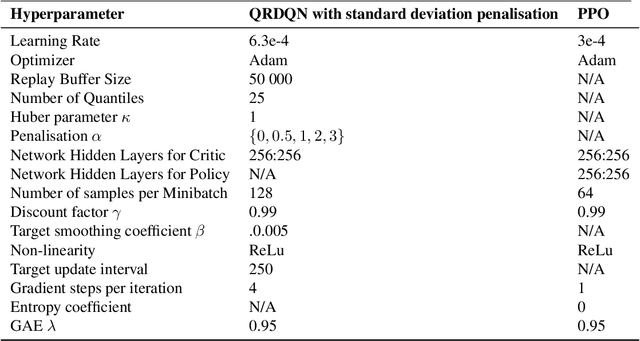
Robust Reinforcement Learning tries to make predictions more robust to changes in the dynamics or rewards of the system. This problem is particularly important when the dynamics and rewards of the environment are estimated from the data. In this paper, we approximate the Robust Reinforcement Learning constrained with a $\Phi$-divergence using an approximate Risk-Averse formulation. We show that the classical Reinforcement Learning formulation can be robustified using standard deviation penalization of the objective. Two algorithms based on Distributional Reinforcement Learning, one for discrete and one for continuous action spaces are proposed and tested in a classical Gym environment to demonstrate the robustness of the algorithms.

Challenging common bolus advisor for self-monitoring type-I diabetes patients using Reinforcement Learning

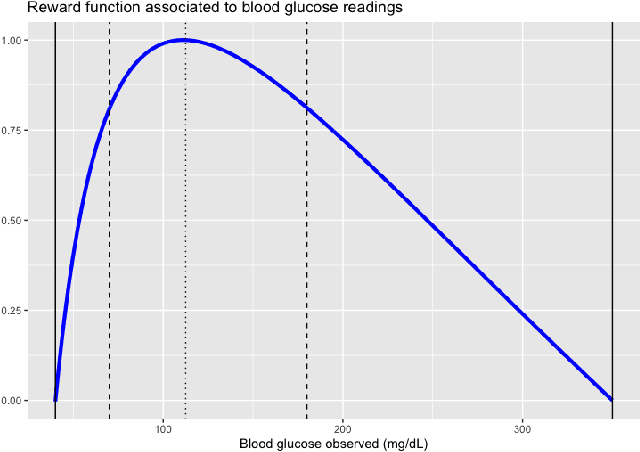
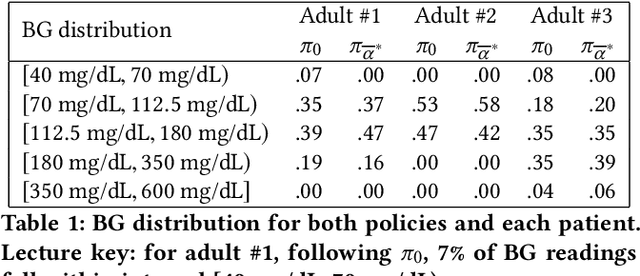
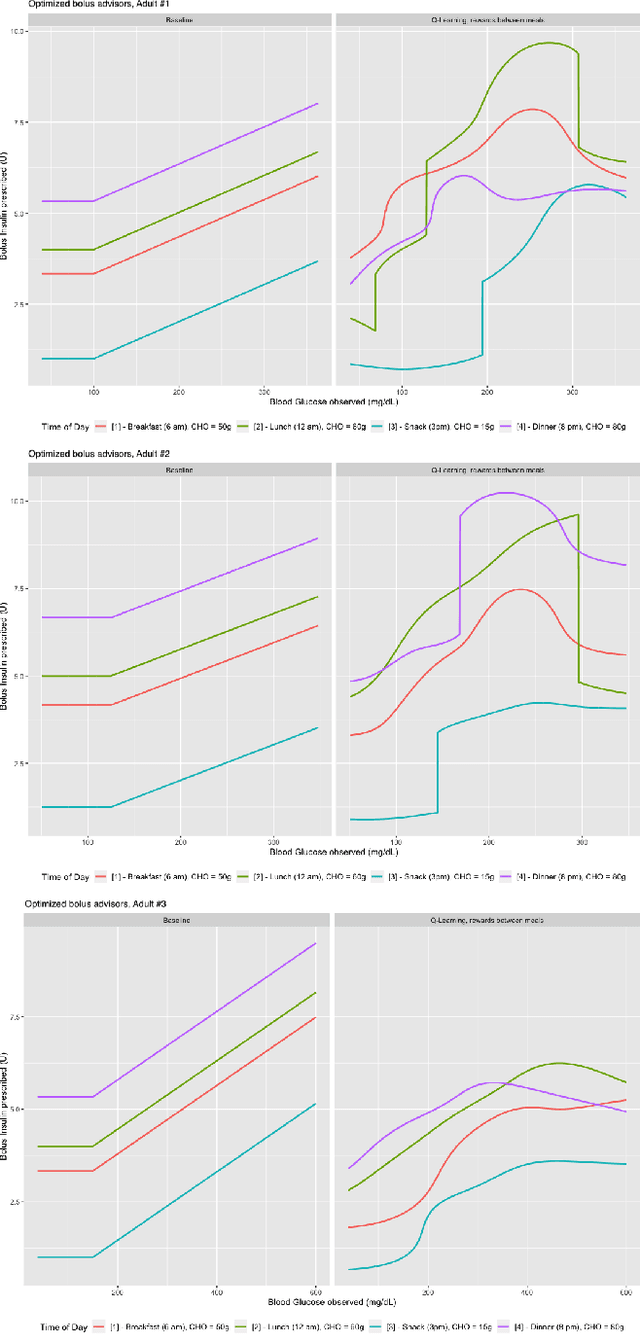
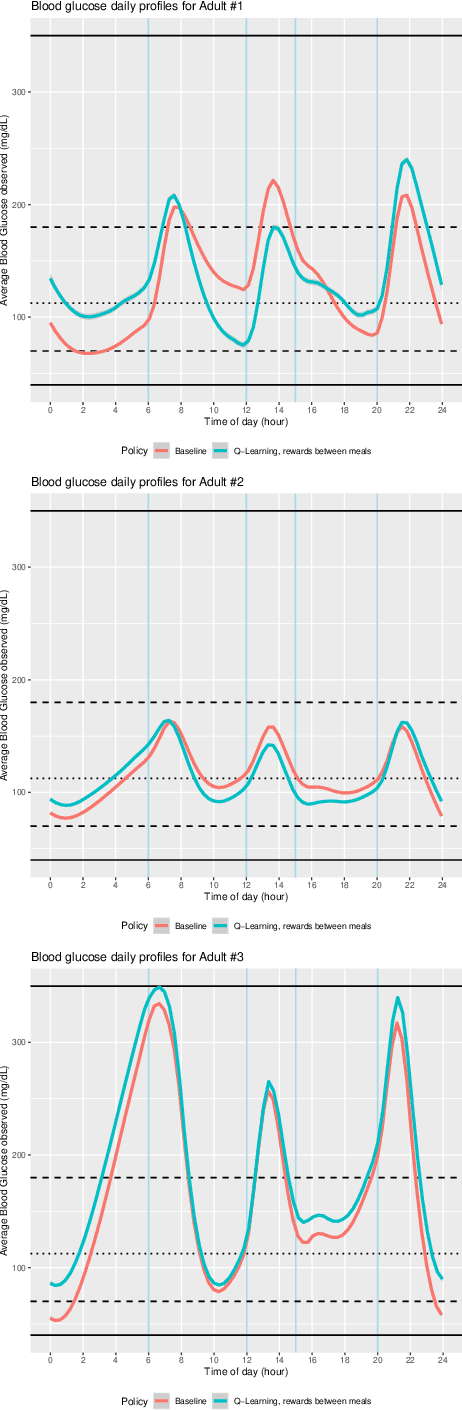
Patients with diabetes who are self-monitoring have to decide right before each meal how much insulin they should take. A standard bolus advisor exists, but has never actually been proven to be optimal in any sense. We challenged this rule applying Reinforcement Learning techniques on data simulated with T1DM, an FDA-approved simulator developed by Kovatchev et al. modeling the gluco-insulin interaction. Results show that the optimal bolus rule is fairly different from the standard bolus advisor, and if followed can actually avoid hypoglycemia episodes.

Learning from both experts and data

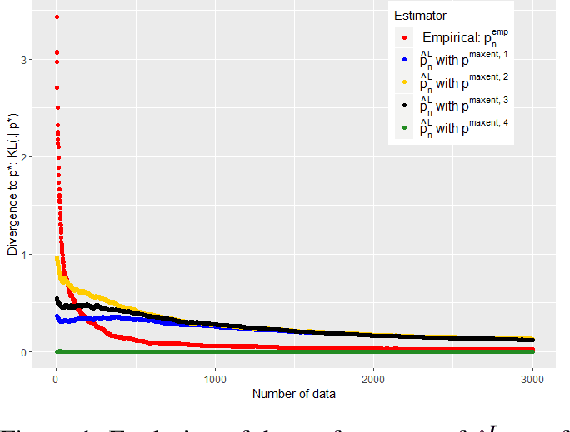
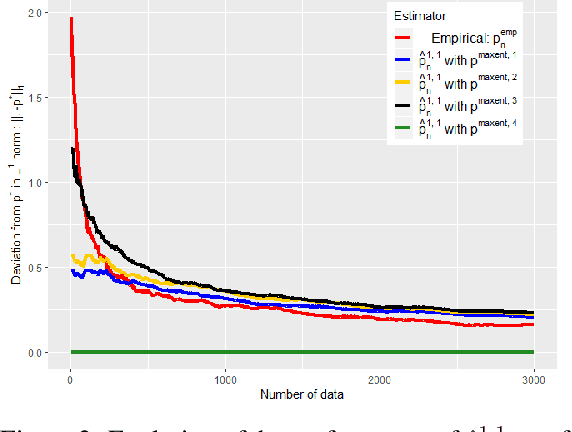
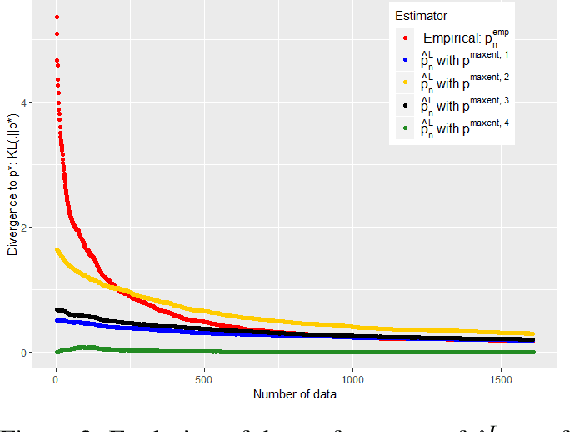
In this work we study the problem of inferring a discrete probability distribution using both expert knowledge and empirical data. This is an important issue for many applications where the scarcity of data prevents a purely empirical approach. In this context, it is common to rely first on an initial domain knowledge a priori before proceeding to an online data acquisition. We are particularly interested in the intermediate regime where we do not have enough data to do without the initial expert a priori of the experts, but enough to correct it if necessary. We present here a novel way to tackle this issue with a method providing an objective way to choose the weight to be given to experts compared to data. We show, both empirically and theoretically, that our proposed estimator is always more efficient than the best of the two models (expert or data) within a constant.

A Model-Based Reinforcement Learning Approach for a Rare Disease Diagnostic Task

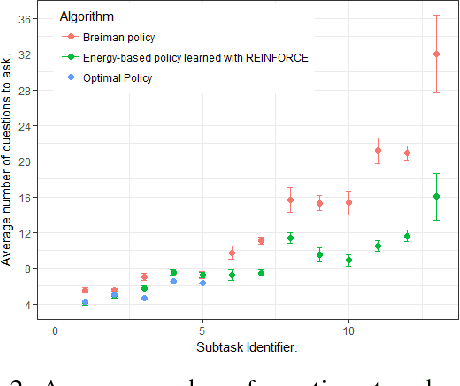
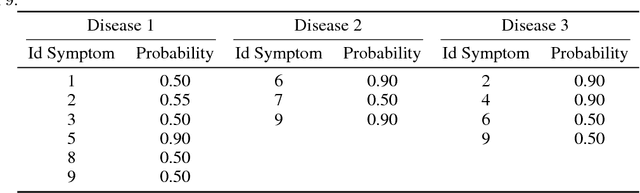
In this work, we present our various contributions to the objective of building a decision support tool for the diagnosis of rare diseases. Our goal is to achieve a state of knowledge where the uncertainty about the patient's disease is below a predetermined threshold. We aim to reach such states while minimizing the average number of medical tests to perform. In doing so, we take into account the need, in many medical applications, to avoid, as much as possible, any misdiagnosis. To solve this optimization task, we investigate several reinforcement learning algorithm and make them operable in our high-dimensional and sparse-reward setting. We also present a way to combine expert knowledge, expressed as conditional probabilities, with real clinical data. This is crucial because the scarcity of data in the field of rare diseases prevents any approach based solely on clinical data. Finally we show that it is possible to integrate the ontological information about symptoms while remaining in our probabilistic reasoning. It enables our decision support tool to process information given at different level of precision by the user.