Robust Reinforcement Learning with Distributional Risk-averse formulation
Paper and Code
Jun 14, 2022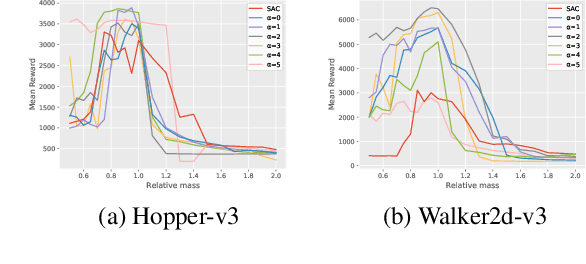


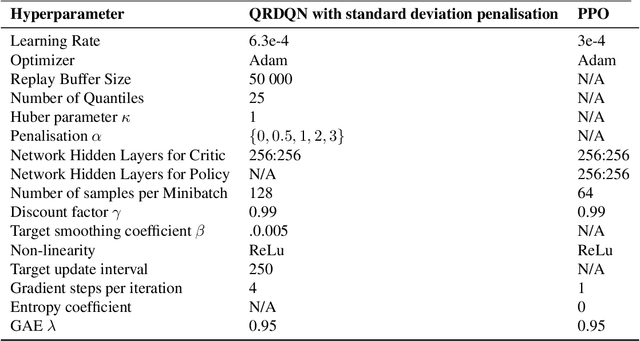
Robust Reinforcement Learning tries to make predictions more robust to changes in the dynamics or rewards of the system. This problem is particularly important when the dynamics and rewards of the environment are estimated from the data. In this paper, we approximate the Robust Reinforcement Learning constrained with a $\Phi$-divergence using an approximate Risk-Averse formulation. We show that the classical Reinforcement Learning formulation can be robustified using standard deviation penalization of the objective. Two algorithms based on Distributional Reinforcement Learning, one for discrete and one for continuous action spaces are proposed and tested in a classical Gym environment to demonstrate the robustness of the algorithms.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge