Markov Logic Networks for Natural Language Question Answering

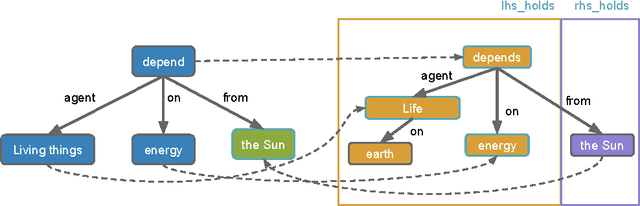
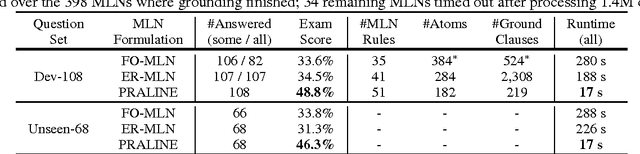
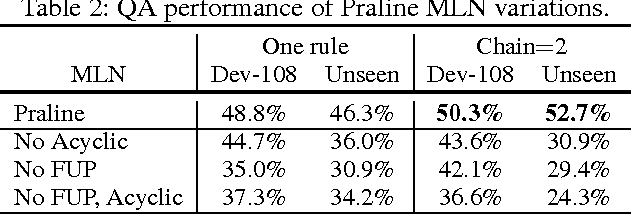
Our goal is to answer elementary-level science questions using knowledge extracted automatically from science textbooks, expressed in a subset of first-order logic. Given the incomplete and noisy nature of these automatically extracted rules, Markov Logic Networks (MLNs) seem a natural model to use, but the exact way of leveraging MLNs is by no means obvious. We investigate three ways of applying MLNs to our task. In the first, we simply use the extracted science rules directly as MLN clauses. Unlike typical MLN applications, our domain has long and complex rules, leading to an unmanageable number of groundings. We exploit the structure present in hard constraints to improve tractability, but the formulation remains ineffective. In the second approach, we instead interpret science rules as describing prototypical entities, thus mapping rules directly to grounded MLN assertions, whose constants are then clustered using existing entity resolution methods. This drastically simplifies the network, but still suffers from brittleness. Finally, our third approach, called Praline, uses MLNs to align the lexical elements as well as define and control how inference should be performed in this task. Our experiments, demonstrating a 15\% accuracy boost and a 10x reduction in runtime, suggest that the flexibility and different inference semantics of Praline are a better fit for the natural language question answering task.

Symmetric Weighted First-Order Model Counting

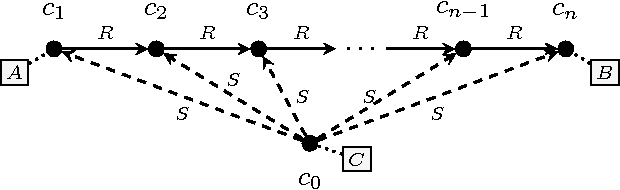
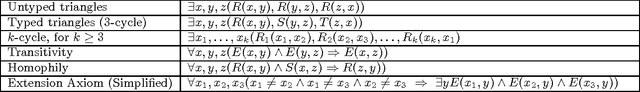
The FO Model Counting problem (FOMC) is the following: given a sentence $\Phi$ in FO and a number $n$, compute the number of models of $\Phi$ over a domain of size $n$; the Weighted variant (WFOMC) generalizes the problem by associating a weight to each tuple and defining the weight of a model to be the product of weights of its tuples. In this paper we study the complexity of the symmetric WFOMC, where all tuples of a given relation have the same weight. Our motivation comes from an important application, inference in Knowledge Bases with soft constraints, like Markov Logic Networks, but the problem is also of independent theoretical interest. We study both the data complexity, and the combined complexity of FOMC and WFOMC. For the data complexity we prove the existence of an FO$^{3}$ formula for which FOMC is #P$_1$-complete, and the existence of a Conjunctive Query for which WFOMC is #P$_1$-complete. We also prove that all $\gamma$-acyclic queries have polynomial time data complexity. For the combined complexity, we prove that, for every fragment FO$^{k}$, $k\geq 2$, the combined complexity of FOMC (or WFOMC) is #P-complete.

Understanding the Complexity of Lifted Inference and Asymmetric Weighted Model Counting

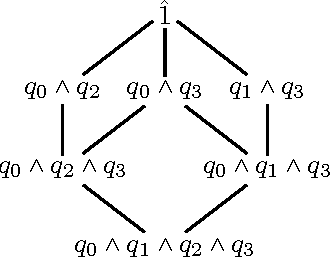
In this paper we study lifted inference for the Weighted First-Order Model Counting problem (WFOMC), which counts the assignments that satisfy a given sentence in first-order logic (FOL); it has applications in Statistical Relational Learning (SRL) and Probabilistic Databases (PDB). We present several results. First, we describe a lifted inference algorithm that generalizes prior approaches in SRL and PDB. Second, we provide a novel dichotomy result for a non-trivial fragment of FO CNF sentences, showing that for each sentence the WFOMC problem is either in PTIME or #P-hard in the size of the input domain; we prove that, in the first case our algorithm solves the WFOMC problem in PTIME, and in the second case it fails. Third, we present several properties of the algorithm. Finally, we discuss limitations of lifted inference for symmetric probabilistic databases (where the weights of ground literals depend only on the relation name, and not on the constants of the domain), and prove the impossibility of a dichotomy result for the complexity of probabilistic inference for the entire language FOL.