MASt3R-SLAM: Real-Time Dense SLAM with 3D Reconstruction Priors

We present a real-time monocular dense SLAM system designed bottom-up from MASt3R, a two-view 3D reconstruction and matching prior. Equipped with this strong prior, our system is robust on in-the-wild video sequences despite making no assumption on a fixed or parametric camera model beyond a unique camera centre. We introduce efficient methods for pointmap matching, camera tracking and local fusion, graph construction and loop closure, and second-order global optimisation. With known calibration, a simple modification to the system achieves state-of-the-art performance across various benchmarks. Altogether, we propose a plug-and-play monocular SLAM system capable of producing globally-consistent poses and dense geometry while operating at 15 FPS.

COMO: Compact Mapping and Odometry

We present COMO, a real-time monocular mapping and odometry system that encodes dense geometry via a compact set of 3D anchor points. Decoding anchor point projections into dense geometry via per-keyframe depth covariance functions guarantees that depth maps are joined together at visible anchor points. The representation enables joint optimization of camera poses and dense geometry, intrinsic 3D consistency, and efficient second-order inference. To maintain a compact yet expressive map, we introduce a frontend that leverages the covariance function for tracking and initializing potentially visually indistinct 3D points across frames. Altogether, we introduce a real-time system capable of estimating accurate poses and consistent geometry.

Learning a Depth Covariance Function

We propose learning a depth covariance function with applications to geometric vision tasks. Given RGB images as input, the covariance function can be flexibly used to define priors over depth functions, predictive distributions given observations, and methods for active point selection. We leverage these techniques for a selection of downstream tasks: depth completion, bundle adjustment, and monocular dense visual odometry.

LEO: Learning Energy-based Models in Graph Optimization

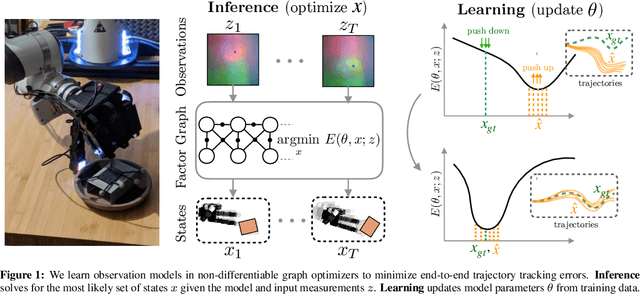
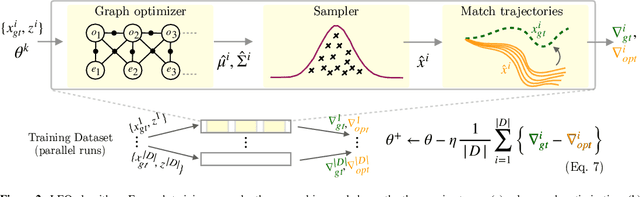
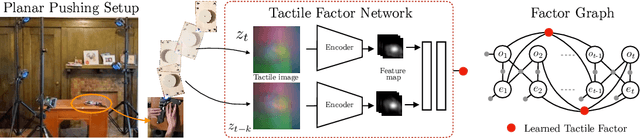
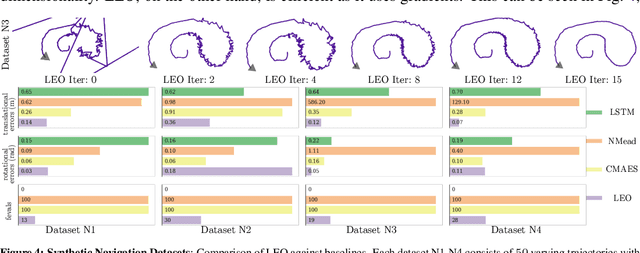
We address the problem of learning observation models end-to-end for estimation. Robots operating in partially observable environments must infer latent states from multiple sensory inputs using observation models that capture the joint distribution between latent states and observations. This inference problem can be formulated as an objective over a graph that optimizes for the most likely sequence of states using all previous measurements. Prior work uses observation models that are either known a-priori or trained on surrogate losses independent of the graph optimizer. In this paper, we propose a method to directly optimize end-to-end tracking performance by learning observation models with the graph optimizer in the loop. This direct approach may appear, however, to require the inference algorithm to be fully differentiable, which many state-of-the-art graph optimizers are not. Our key insight is to instead formulate the problem as that of energy-based learning. We propose a novel approach, LEO, for learning observation models end-to-end with non-differentiable graph optimizers. LEO alternates between sampling trajectories from the graph posterior and updating the model to match these samples to ground truth trajectories. We propose a way to generate such samples efficiently using incremental Gauss-Newton solvers. We compare LEO against baselines on datasets drawn from two distinct tasks: navigation and real-world planar pushing. We show that LEO is able to learn complex observation models with lower errors and fewer samples. Supplementary video: https://youtu.be/qWcH9CBXs5c