Eric Bunch
Efficient Document Image Classification Using Region-Based Graph Neural Network
Jun 25, 2021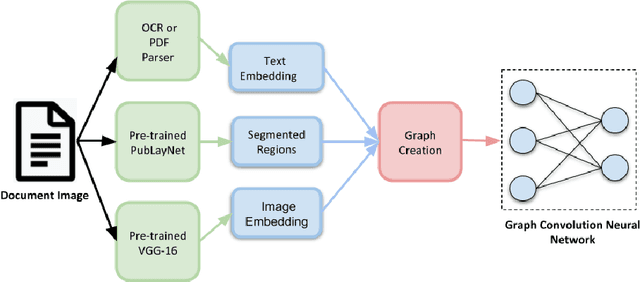
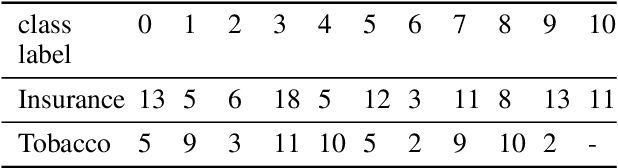

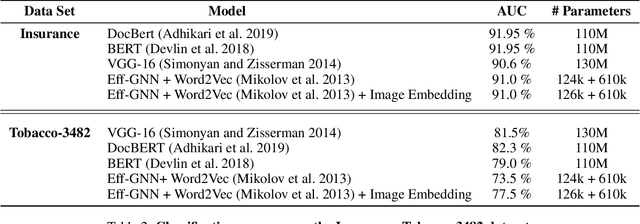
Abstract:Document image classification remains a popular research area because it can be commercialized in many enterprise applications across different industries. Recent advancements in large pre-trained computer vision and language models and graph neural networks has lent document image classification many tools. However using large pre-trained models usually requires substantial computing resources which could defeat the cost-saving advantages of automatic document image classification. In the paper we propose an efficient document image classification framework that uses graph convolution neural networks and incorporates textual, visual and layout information of the document. We have rigorously benchmarked our proposed algorithm against several state-of-art vision and language models on both publicly available dataset and a real-life insurance document classification dataset. Empirical results on both publicly available and real-world data show that our methods achieve near SOTA performance yet require much less computing resources and time for model training and inference. This results in solutions than offer better cost advantages, especially in scalable deployment for enterprise applications. The results showed that our algorithm can achieve classification performance quite close to SOTA. We also provide comprehensive comparisons of computing resources, model sizes, train and inference time between our proposed methods and baselines. In addition we delineate the cost per image using our method and other baselines.
Weighting vectors for machine learning: numerical harmonic analysis applied to boundary detection
Jun 01, 2021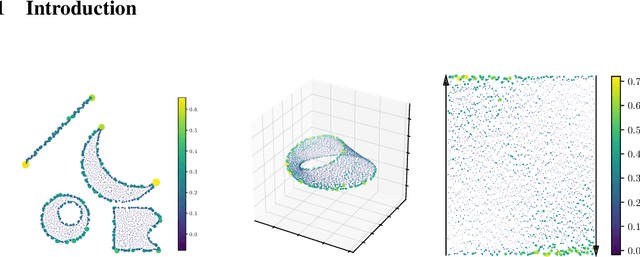


Abstract:Metric space magnitude, an active field of research in algebraic topology, is a scalar quantity that summarizes the effective number of distinct points that live in a general metric space. The {\em weighting vector} is a closely-related concept that captures, in a nontrivial way, much of the underlying geometry of the original metric space. Recent work has demonstrated that when the metric space is Euclidean, the weighting vector serves as an effective tool for boundary detection. We recast this result and show the weighting vector may be viewed as a solution to a kernelized SVM. As one consequence, we apply this new insight to the task of outlier detection, and we demonstrate performance that is competitive or exceeds performance of state-of-the-art techniques on benchmark data sets. Under mild assumptions, we show the weighting vector, which has computational cost of matrix inversion, can be efficiently approximated in linear time. We show how nearest neighbor methods can approximate solutions to the minimization problems defined by SVMs.
Geometric feature performance under downsampling for EEG classification tasks
Feb 15, 2021

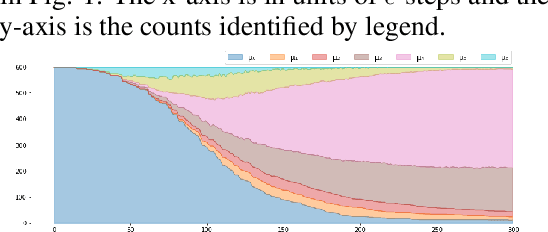
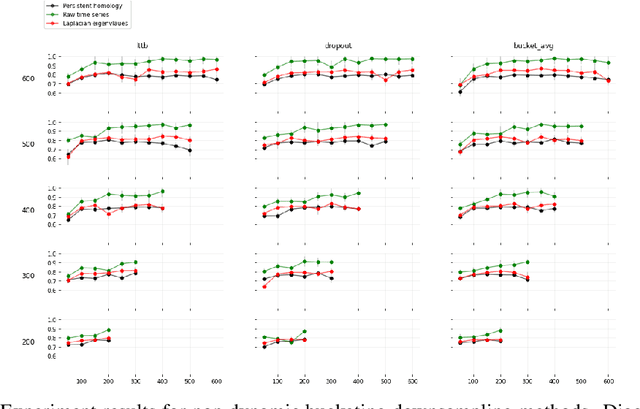
Abstract:We experimentally investigate a collection of feature engineering pipelines for use with a CNN for classifying eyes-open or eyes-closed from electroencephalogram (EEG) time-series from the Bonn dataset. Using the Takens' embedding--a geometric representation of time-series--we construct simplicial complexes from EEG data. We then compare $\epsilon$-series of Betti-numbers and $\epsilon$-series of graph spectra (a novel construction)--two topological invariants of the latent geometry from these complexes--to raw time series of the EEG to fill in a gap in the literature for benchmarking. These methods, inspired by Topological Data Analysis, are used for feature engineering to capture local geometry of the time-series. Additionally, we test these feature pipelines' robustness to downsampling and data reduction. This paper seeks to establish clearer expectations for both time-series classification via geometric features, and how CNNs for time-series respond to data of degraded resolution.
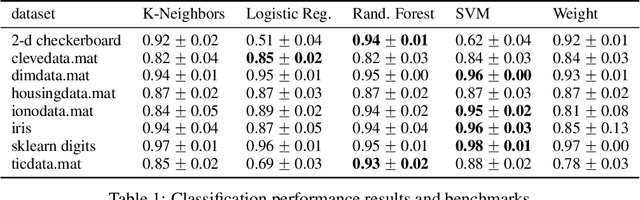
Practical applications of metric space magnitude and weighting vectors
Jul 02, 2020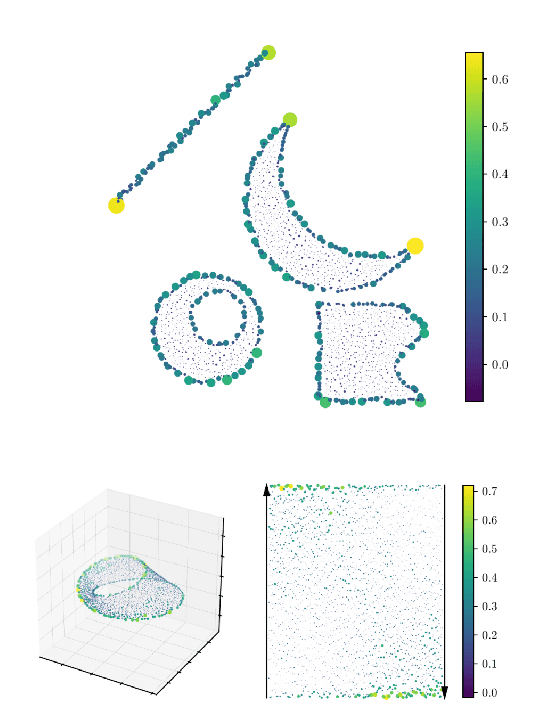
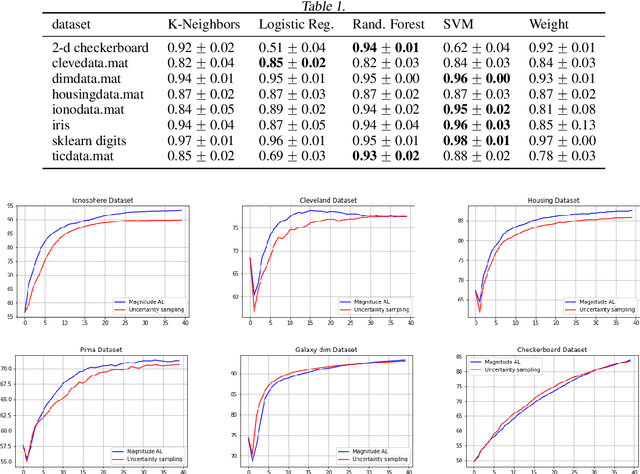

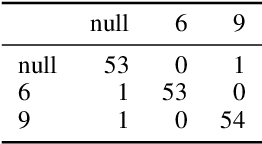
Abstract:Metric space magnitude, an active subject of research in algebraic topology, originally arose in the context of biology, where it was used to represent the effective number of distinct species in an environment. In a more general setting, the magnitude of a metric space is a real number that aims to quantify the effective number of distinct points in the space. The contribution of each point to a metric space's global magnitude, which is encoded by the {\em weighting vector}, captures much of the underlying geometry of the original metric space. Surprisingly, when the metric space is Euclidean, the weighting vector also serves as an effective tool for boundary detection. This allows the weighting vector to serve as the foundation of novel algorithms for classic machine learning tasks such as classification, outlier detection and active learning. We demonstrate, using experiments and comparisons on classic benchmark datasets, the promise of the proposed magnitude and weighting vector-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge