Bryan Bischof
Geometric feature performance under downsampling for EEG classification tasks
Feb 15, 2021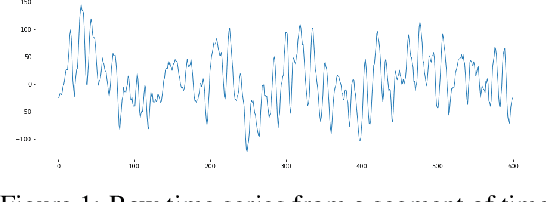

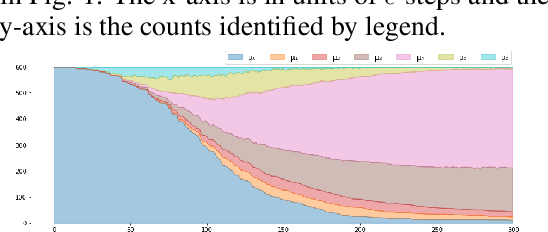
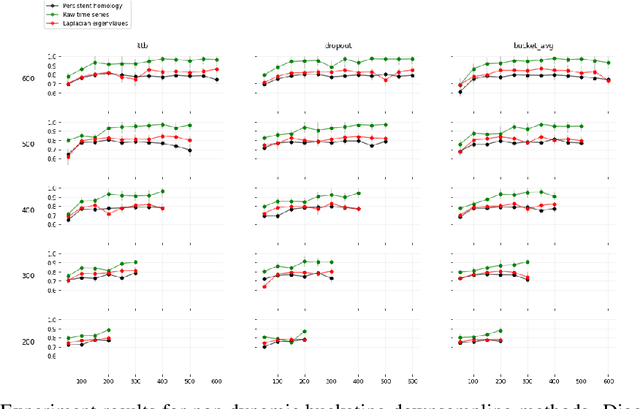
Abstract:We experimentally investigate a collection of feature engineering pipelines for use with a CNN for classifying eyes-open or eyes-closed from electroencephalogram (EEG) time-series from the Bonn dataset. Using the Takens' embedding--a geometric representation of time-series--we construct simplicial complexes from EEG data. We then compare $\epsilon$-series of Betti-numbers and $\epsilon$-series of graph spectra (a novel construction)--two topological invariants of the latent geometry from these complexes--to raw time series of the EEG to fill in a gap in the literature for benchmarking. These methods, inspired by Topological Data Analysis, are used for feature engineering to capture local geometry of the time-series. Additionally, we test these feature pipelines' robustness to downsampling and data reduction. This paper seeks to establish clearer expectations for both time-series classification via geometric features, and how CNNs for time-series respond to data of degraded resolution.
Higher order co-occurrence tensors for hypergraphs via face-splitting
Feb 15, 2020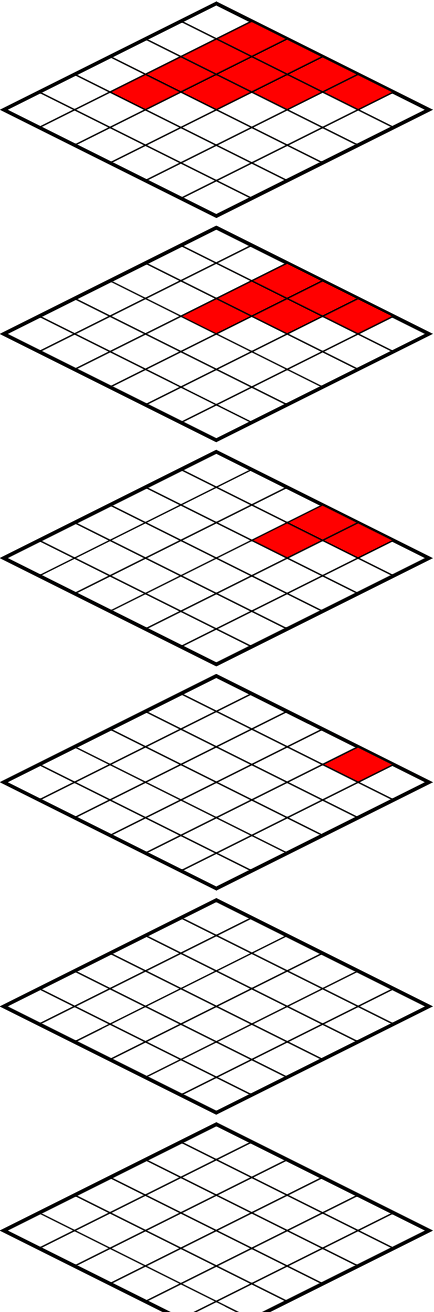
Abstract:A popular trick for computing a pairwise co-occurrence matrix is the product of an incidence matrix and its transpose. We present an analog for higher order tuple co-occurrences using the face-splitting product, or alternately known as the transpose Khatri-Rao product. These higher order co-occurrences encode the commonality of tokens in the company of other tokens, and thus generalize the mutual information commonly studied. We demonstrate this tensor's use via a popular NLP model, and hypergraph models of similarity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge