Assessing Resource-Performance Trade-off of Natural Language Models using Data Envelopment Analysis

Natural language models are often summarized through a high-dimensional set of descriptive metrics including training corpus size, training time, the number of trainable parameters, inference times, and evaluation statistics that assess performance across tasks. The high dimensional nature of these metrics yields challenges with regard to objectively comparing models; in particular it is challenging to assess the trade-off models make between performance and resources (compute time, memory, etc.). We apply Data Envelopment Analysis (DEA) to this problem of assessing the resource-performance trade-off. DEA is a nonparametric method that measures productive efficiency of abstract units that consume one or more inputs and yield at least one output. We recast natural language models as units suitable for DEA, and we show that DEA can be used to create an effective framework for quantifying model performance and efficiency. A central feature of DEA is that it identifies a subset of models that live on an efficient frontier of performance. DEA is also scalable, having been applied to problems with thousands of units. We report empirical results of DEA applied to 14 different language models that have a variety of architectures, and we show that DEA can be used to identify a subset of models that effectively balance resource demands against performance.

Multi Resolution Analysis (MRA) for Approximate Self-Attention

Transformers have emerged as a preferred model for many tasks in natural langugage processing and vision. Recent efforts on training and deploying Transformers more efficiently have identified many strategies to approximate the self-attention matrix, a key module in a Transformer architecture. Effective ideas include various prespecified sparsity patterns, low-rank basis expansions and combinations thereof. In this paper, we revisit classical Multiresolution Analysis (MRA) concepts such as Wavelets, whose potential value in this setting remains underexplored thus far. We show that simple approximations based on empirical feedback and design choices informed by modern hardware and implementation challenges, eventually yield a MRA-based approach for self-attention with an excellent performance profile across most criteria of interest. We undertake an extensive set of experiments and demonstrate that this multi-resolution scheme outperforms most efficient self-attention proposals and is favorable for both short and long sequences. Code is available at \url{https://github.com/mlpen/mra-attention}.

Weighting vectors for machine learning: numerical harmonic analysis applied to boundary detection

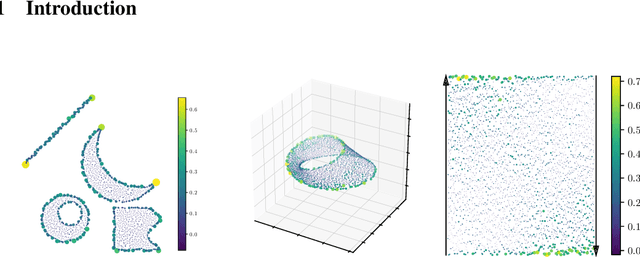
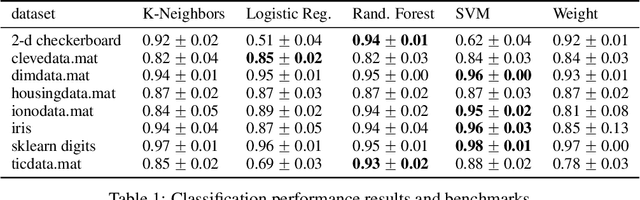
Metric space magnitude, an active field of research in algebraic topology, is a scalar quantity that summarizes the effective number of distinct points that live in a general metric space. The {\em weighting vector} is a closely-related concept that captures, in a nontrivial way, much of the underlying geometry of the original metric space. Recent work has demonstrated that when the metric space is Euclidean, the weighting vector serves as an effective tool for boundary detection. We recast this result and show the weighting vector may be viewed as a solution to a kernelized SVM. As one consequence, we apply this new insight to the task of outlier detection, and we demonstrate performance that is competitive or exceeds performance of state-of-the-art techniques on benchmark data sets. Under mild assumptions, we show the weighting vector, which has computational cost of matrix inversion, can be efficiently approximated in linear time. We show how nearest neighbor methods can approximate solutions to the minimization problems defined by SVMs.

Practical applications of metric space magnitude and weighting vectors

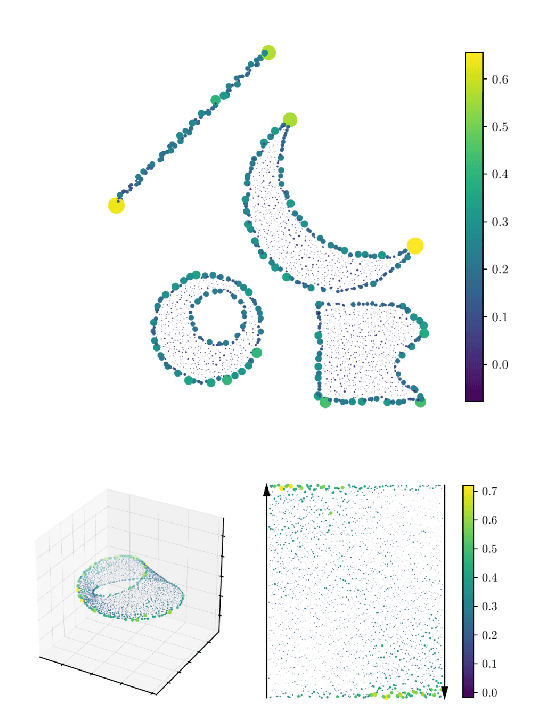
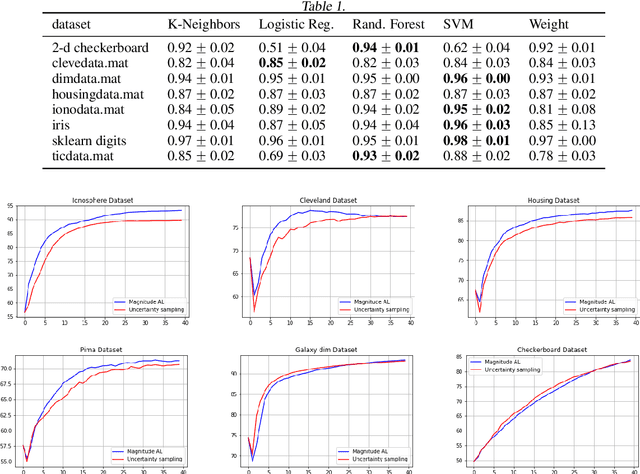
Metric space magnitude, an active subject of research in algebraic topology, originally arose in the context of biology, where it was used to represent the effective number of distinct species in an environment. In a more general setting, the magnitude of a metric space is a real number that aims to quantify the effective number of distinct points in the space. The contribution of each point to a metric space's global magnitude, which is encoded by the {\em weighting vector}, captures much of the underlying geometry of the original metric space. Surprisingly, when the metric space is Euclidean, the weighting vector also serves as an effective tool for boundary detection. This allows the weighting vector to serve as the foundation of novel algorithms for classic machine learning tasks such as classification, outlier detection and active learning. We demonstrate, using experiments and comparisons on classic benchmark datasets, the promise of the proposed magnitude and weighting vector-based approaches.