Mechanism Design for Efficient Online and Offline Allocation of Electric Vehicles to Charging Stations

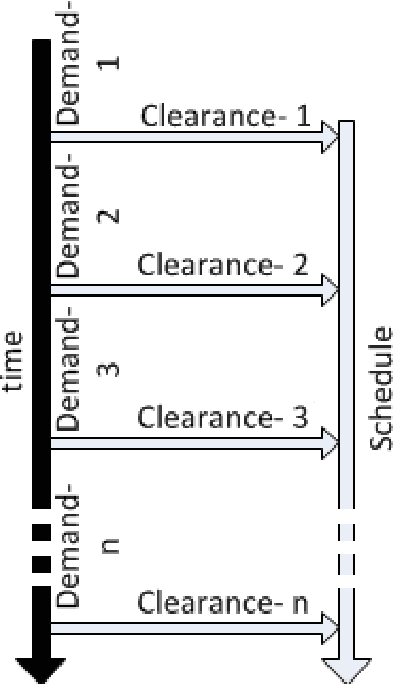
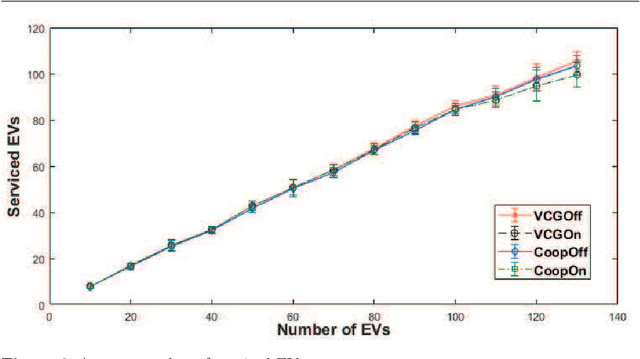
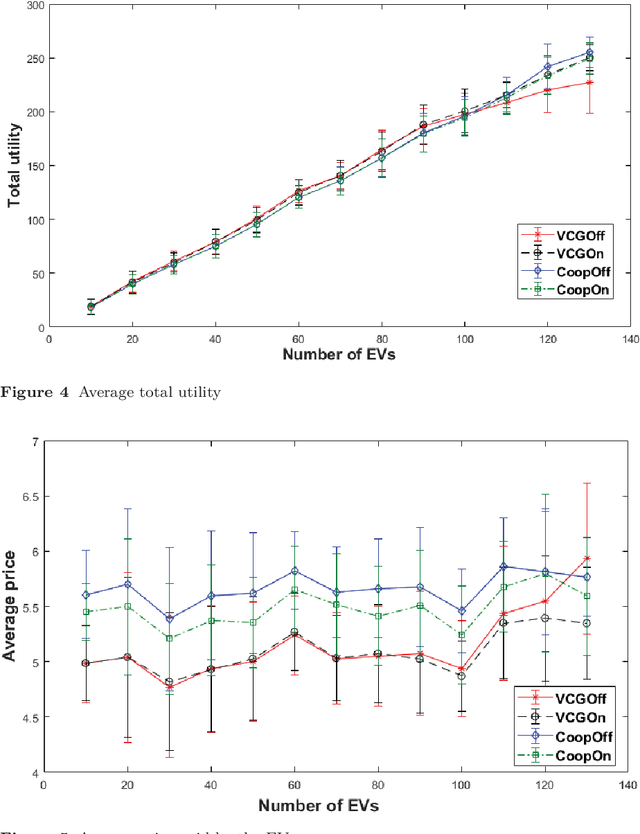
We study the problem of allocating Electric Vehicles (EVs) to charging stations and scheduling their charging. We develop offline and online solutions that treat EV users as self-interested agents that aim to maximise their profit and minimise the impact on their schedule. We formulate the problem of the optimal EV to charging station allocation as a Mixed Integer Programming (MIP) one and we propose two pricing mechanisms: A fixed-price one, and another that is based on the well known Vickrey-Clark-Groves (VCG) mechanism. Later, we develop online solutions that incrementally call the MIP-based algorithm. We empirically evaluate our mechanisms and we observe that both scale well. Moreover, the VCG mechanism services on average $1.5\%$ more EVs than the fixed-price one. In addition, when the stations get congested, VCG leads to higher prices for the EVs and higher profit for the stations, but lower utility for the EVs. However, we theoretically prove that the VCG mechanism guarantees truthful reporting of the EVs' preferences. In contrast, the fixed-price one is vulnerable to agents' strategic behaviour as non-truthful EVs can charge in place of truthful ones. Finally, we observe that the online algorithms are on average at $98\%$ of the optimal in EV satisfaction.

Extending the Multiple Traveling Salesman Problem for Scheduling a Fleet of Drones Performing Monitoring Missions

In this paper we schedule the travel path of a set of drones across a graph where the nodes need to be visited multiple times at pre-defined points in time. This is an extension of the well-known multiple traveling salesman problem. The proposed formulation can be applied in several domains such as the monitoring of traffic flows in a transportation network, or the monitoring of remote locations to assist search and rescue missions. Aiming to find the optimal schedule, the problem is formulated as an Integer Linear Program (ILP). Given that the problem is highly combinatorial, the optimal solution scales only for small sized problems. Thus, a greedy algorithm is also proposed that uses a one-step look ahead heuristic search mechanism. In a detailed evaluation, it is observed that the greedy algorithm has near-optimal performance as it is on average at 92.06% of the optimal, while it can potentially scale up to settings with hundreds of drones and locations.