The Price of Pessimism for Automated Defense

The well-worn George Box aphorism ``all models are wrong, but some are useful'' is particularly salient in the cybersecurity domain, where the assumptions built into a model can have substantial financial or even national security impacts. Computer scientists are often asked to optimize for worst-case outcomes, and since security is largely focused on risk mitigation, preparing for the worst-case scenario appears rational. In this work, we demonstrate that preparing for the worst case rather than the most probable case may yield suboptimal outcomes for learning agents. Through the lens of stochastic Bayesian games, we first explore different attacker knowledge modeling assumptions that impact the usefulness of models to cybersecurity practitioners. By considering different models of attacker knowledge about the state of the game and a defender's hidden information, we find that there is a cost to the defender for optimizing against the worst case.

Simulation of Attacker Defender Interaction in a Noisy Security Game

In the cybersecurity setting, defenders are often at the mercy of their detection technologies and subject to the information and experiences that individual analysts have. In order to give defenders an advantage, it is important to understand an attacker's motivation and their likely next best action. As a first step in modeling this behavior, we introduce a security game framework that simulates interplay between attackers and defenders in a noisy environment, focusing on the factors that drive decision making for attackers and defenders in the variants of the game with full knowledge and observability, knowledge of the parameters but no observability of the state (``partial knowledge''), and zero knowledge or observability (``zero knowledge''). We demonstrate the importance of making the right assumptions about attackers, given significant differences in outcomes. Furthermore, there is a measurable trade-off between false-positives and true-positives in terms of attacker outcomes, suggesting that a more false-positive prone environment may be acceptable under conditions where true-positives are also higher.

Eliciting Information with Partial Signals in Repeated Games

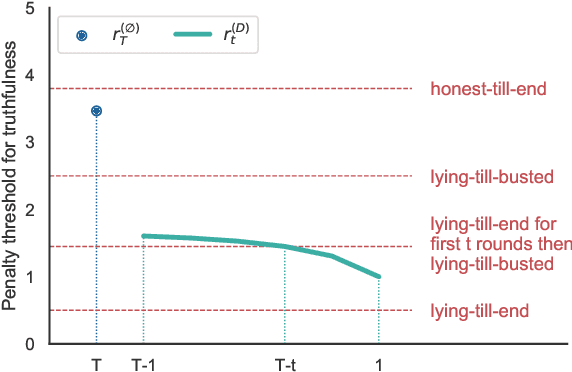
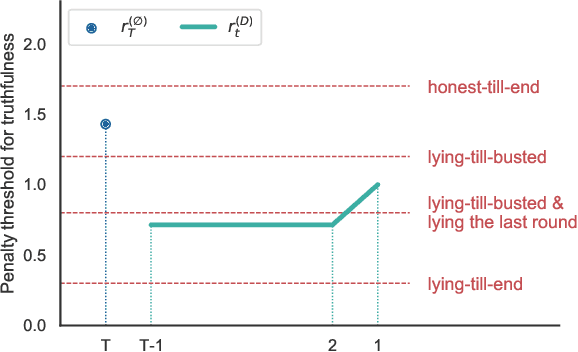
We consider an information elicitation game where the center needs the agent to self-report her actual usage of a service and charges her a payment accordingly. The center can only observe a partial signal, representing part of the agent's true consumption, that is generated randomly from a publicly known distribution. The agent can report any information, as long as it does not contradict the signal, and the center issues a payment based on the reported information. Such problems find application in prosumer pricing, tax filing, etc., when the agent's actual consumption of a service is masked from the center and verification of the submitted reports is impractical. The key difference between the current problem and classic information elicitation problems is that the agent gets to observe the full signal and act strategically, but the center can only see the partial signal. For this seemingly impossible problem, we propose a penalty mechanism that elicits truthful self-reports in a repeated game. In particular, besides charging the agent the reported value, the mechanism charges a penalty proportional to her inconsistent reports. We show how a combination of the penalty rate and the length of the game incentivizes the agent to be truthful for the entire game, a phenomenon we call "fear of tomorrow verification". We show how approximate results for arbitrary distributions can be obtained by analyzing Bernoulli distributions. We extend our mechanism to a multi-agent cost sharing setting and give equilibrium results.