Eliciting Information with Partial Signals in Repeated Games

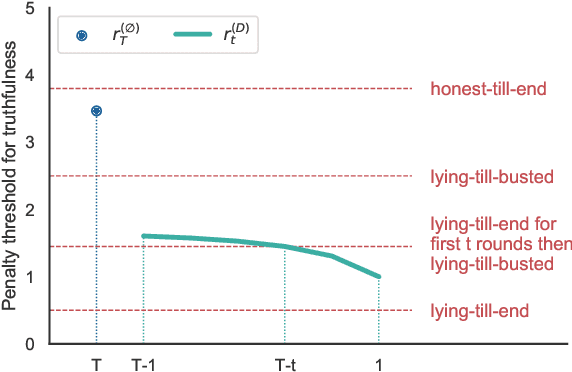
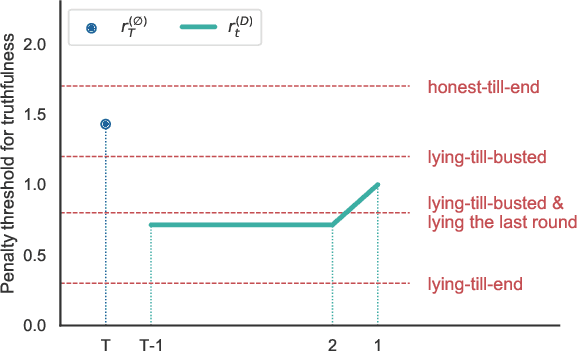
We consider an information elicitation game where the center needs the agent to self-report her actual usage of a service and charges her a payment accordingly. The center can only observe a partial signal, representing part of the agent's true consumption, that is generated randomly from a publicly known distribution. The agent can report any information, as long as it does not contradict the signal, and the center issues a payment based on the reported information. Such problems find application in prosumer pricing, tax filing, etc., when the agent's actual consumption of a service is masked from the center and verification of the submitted reports is impractical. The key difference between the current problem and classic information elicitation problems is that the agent gets to observe the full signal and act strategically, but the center can only see the partial signal. For this seemingly impossible problem, we propose a penalty mechanism that elicits truthful self-reports in a repeated game. In particular, besides charging the agent the reported value, the mechanism charges a penalty proportional to her inconsistent reports. We show how a combination of the penalty rate and the length of the game incentivizes the agent to be truthful for the entire game, a phenomenon we call "fear of tomorrow verification". We show how approximate results for arbitrary distributions can be obtained by analyzing Bernoulli distributions. We extend our mechanism to a multi-agent cost sharing setting and give equilibrium results.

Maximizing Non-Monotone DR-Submodular Functions with Cardinality Constraints

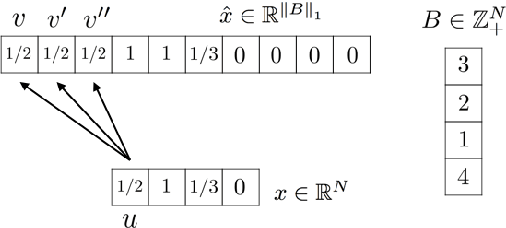
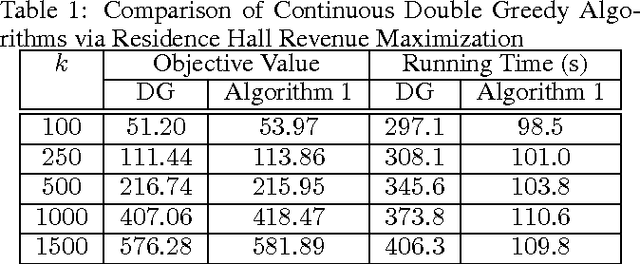
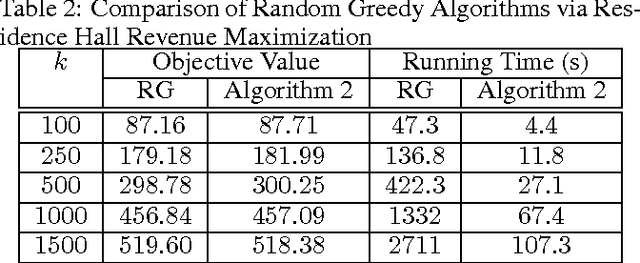
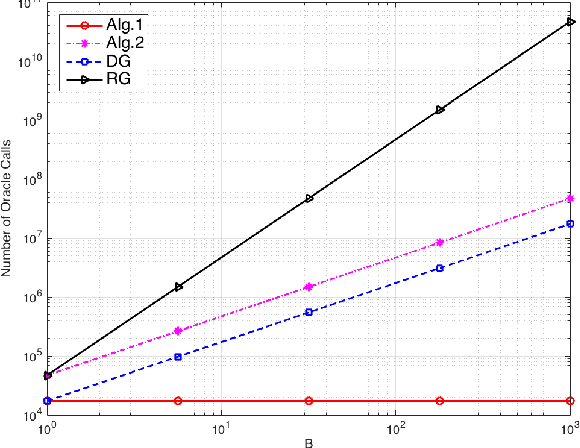
We consider the problem of maximizing a non-monotone DR-submodular function subject to a cardinality constraint. Diminishing returns (DR) submodularity is a generalization of the diminishing returns property for functions defined over the integer lattice. This generalization can be used to solve many machine learning or combinatorial optimization problems such as optimal budget allocation, revenue maximization, etc. In this work we propose the first polynomial-time approximation algorithms for non-monotone constrained maximization. We implement our algorithms for a revenue maximization problem with a real-world dataset to check their efficiency and performance.