AFLGuard: Byzantine-robust Asynchronous Federated Learning

Federated learning (FL) is an emerging machine learning paradigm, in which clients jointly learn a model with the help of a cloud server. A fundamental challenge of FL is that the clients are often heterogeneous, e.g., they have different computing powers, and thus the clients may send model updates to the server with substantially different delays. Asynchronous FL aims to address this challenge by enabling the server to update the model once any client's model update reaches it without waiting for other clients' model updates. However, like synchronous FL, asynchronous FL is also vulnerable to poisoning attacks, in which malicious clients manipulate the model via poisoning their local data and/or model updates sent to the server. Byzantine-robust FL aims to defend against poisoning attacks. In particular, Byzantine-robust FL can learn an accurate model even if some clients are malicious and have Byzantine behaviors. However, most existing studies on Byzantine-robust FL focused on synchronous FL, leaving asynchronous FL largely unexplored. In this work, we bridge this gap by proposing AFLGuard, a Byzantine-robust asynchronous FL method. We show that, both theoretically and empirically, AFLGuard is robust against various existing and adaptive poisoning attacks (both untargeted and targeted). Moreover, AFLGuard outperforms existing Byzantine-robust asynchronous FL methods.

CFedAvg: Achieving Efficient Communication and Fast Convergence in Non-IID Federated Learning

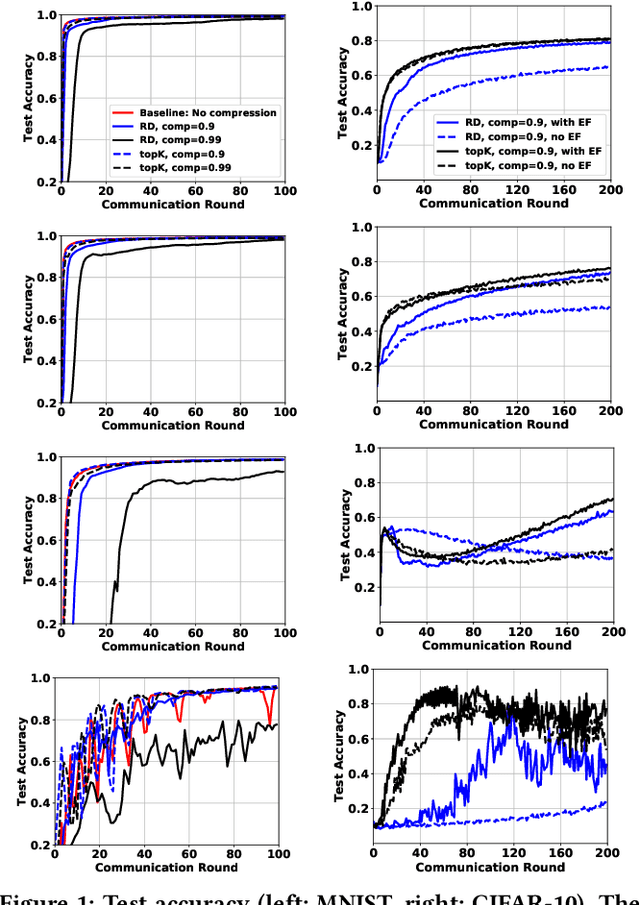
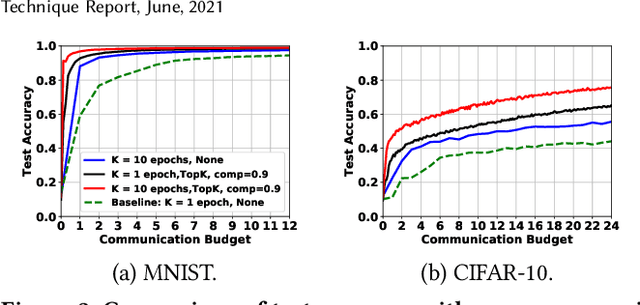
Federated learning (FL) is a prevailing distributed learning paradigm, where a large number of workers jointly learn a model without sharing their training data. However, high communication costs could arise in FL due to large-scale (deep) learning models and bandwidth-constrained connections. In this paper, we introduce a communication-efficient algorithmic framework called CFedAvg for FL with non-i.i.d. datasets, which works with general (biased or unbiased) SNR-constrained compressors. We analyze the convergence rate of CFedAvg for non-convex functions with constant and decaying learning rates. The CFedAvg algorithm can achieve an $\mathcal{O}(1 / \sqrt{mKT} + 1 / T)$ convergence rate with a constant learning rate, implying a linear speedup for convergence as the number of workers increases, where $K$ is the number of local steps, $T$ is the number of total communication rounds, and $m$ is the total worker number. This matches the convergence rate of distributed/federated learning without compression, thus achieving high communication efficiency while not sacrificing learning accuracy in FL. Furthermore, we extend CFedAvg to cases with heterogeneous local steps, which allows different workers to perform a different number of local steps to better adapt to their own circumstances. The interesting observation in general is that the noise/variance introduced by compressors does not affect the overall convergence rate order for non-i.i.d. FL. We verify the effectiveness of our CFedAvg algorithm on three datasets with two gradient compression schemes of different compression ratios.

GT-STORM: Taming Sample, Communication, and Memory Complexities in Decentralized Non-Convex Learning

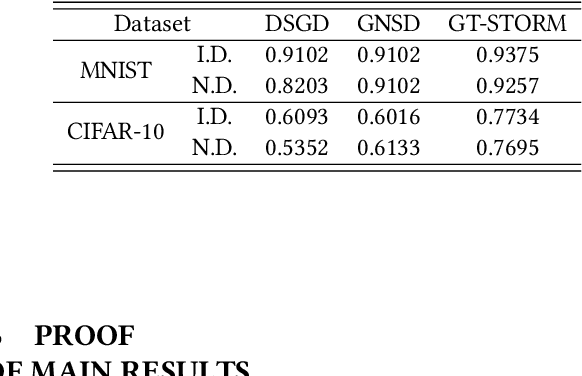
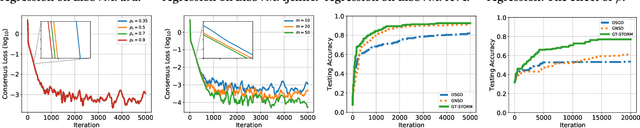
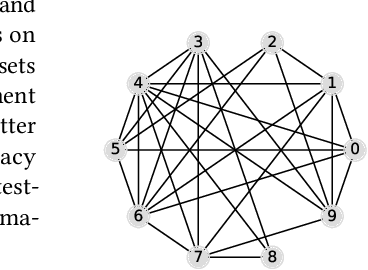
Decentralized nonconvex optimization has received increasing attention in recent years in machine learning due to its advantages in system robustness, data privacy, and implementation simplicity. However, three fundamental challenges in designing decentralized optimization algorithms are how to reduce their sample, communication, and memory complexities. In this paper, we propose a \underline{g}radient-\underline{t}racking-based \underline{sto}chastic \underline{r}ecursive \underline{m}omentum (GT-STORM) algorithm for efficiently solving nonconvex optimization problems. We show that to reach an $\epsilon^2$-stationary solution, the total number of sample evaluations of our algorithm is $\tilde{O}(m^{1/2}\epsilon^{-3})$ and the number of communication rounds is $\tilde{O}(m^{-1/2}\epsilon^{-3})$, which improve the $O(\epsilon^{-4})$ costs of sample evaluations and communications for the existing decentralized stochastic gradient algorithms. We conduct extensive experiments with a variety of learning models, including non-convex logistical regression and convolutional neural networks, to verify our theoretical findings. Collectively, our results contribute to the state of the art of theories and algorithms for decentralized network optimization.