CFedAvg: Achieving Efficient Communication and Fast Convergence in Non-IID Federated Learning
Paper and Code
Jun 14, 2021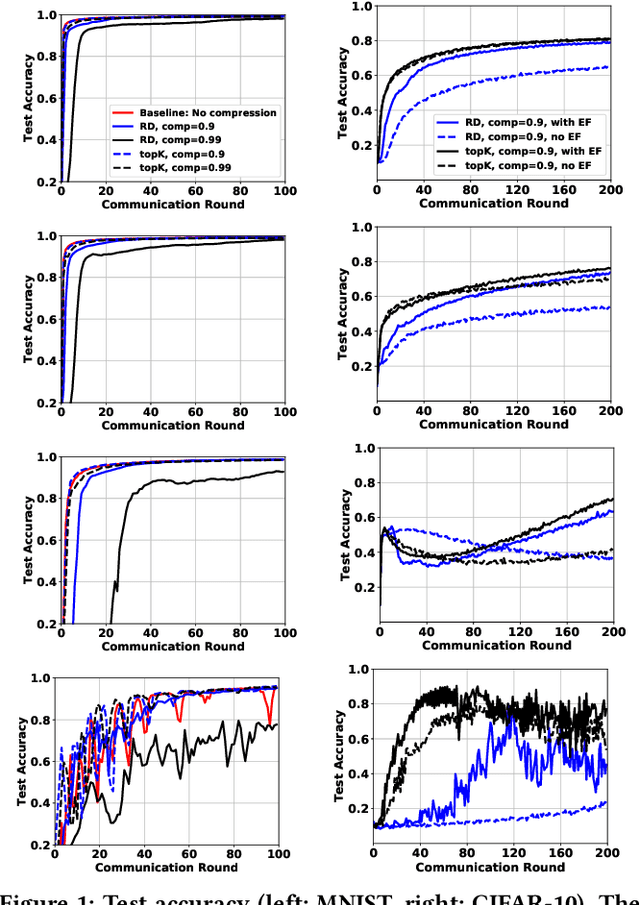

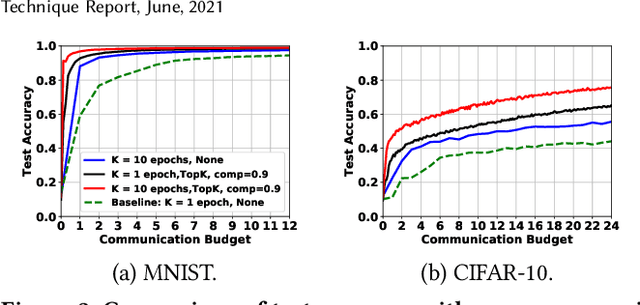

Federated learning (FL) is a prevailing distributed learning paradigm, where a large number of workers jointly learn a model without sharing their training data. However, high communication costs could arise in FL due to large-scale (deep) learning models and bandwidth-constrained connections. In this paper, we introduce a communication-efficient algorithmic framework called CFedAvg for FL with non-i.i.d. datasets, which works with general (biased or unbiased) SNR-constrained compressors. We analyze the convergence rate of CFedAvg for non-convex functions with constant and decaying learning rates. The CFedAvg algorithm can achieve an $\mathcal{O}(1 / \sqrt{mKT} + 1 / T)$ convergence rate with a constant learning rate, implying a linear speedup for convergence as the number of workers increases, where $K$ is the number of local steps, $T$ is the number of total communication rounds, and $m$ is the total worker number. This matches the convergence rate of distributed/federated learning without compression, thus achieving high communication efficiency while not sacrificing learning accuracy in FL. Furthermore, we extend CFedAvg to cases with heterogeneous local steps, which allows different workers to perform a different number of local steps to better adapt to their own circumstances. The interesting observation in general is that the noise/variance introduced by compressors does not affect the overall convergence rate order for non-i.i.d. FL. We verify the effectiveness of our CFedAvg algorithm on three datasets with two gradient compression schemes of different compression ratios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge