Online Control of Unknown Time-Varying Dynamical Systems

We study online control of time-varying linear systems with unknown dynamics in the nonstochastic control model. At a high level, we demonstrate that this setting is \emph{qualitatively harder} than that of either unknown time-invariant or known time-varying dynamics, and complement our negative results with algorithmic upper bounds in regimes where sublinear regret is possible. More specifically, we study regret bounds with respect to common classes of policies: Disturbance Action (SLS), Disturbance Response (Youla), and linear feedback policies. While these three classes are essentially equivalent for LTI systems, we demonstrate that these equivalences break down for time-varying systems. We prove a lower bound that no algorithm can obtain sublinear regret with respect to the first two classes unless a certain measure of system variability also scales sublinearly in the horizon. Furthermore, we show that offline planning over the state linear feedback policies is NP-hard, suggesting hardness of the online learning problem. On the positive side, we give an efficient algorithm that attains a sublinear regret bound against the class of Disturbance Response policies up to the aforementioned system variability term. In fact, our algorithm enjoys sublinear \emph{adaptive} regret bounds, which is a strictly stronger metric than standard regret and is more appropriate for time-varying systems. We sketch extensions to Disturbance Action policies and partial observation, and propose an inefficient algorithm for regret against linear state feedback policies.

Machine Learning for Mechanical Ventilation Control (Extended Abstract)

Mechanical ventilation is one of the most widely used therapies in the ICU. However, despite broad application from anaesthesia to COVID-related life support, many injurious challenges remain. We frame these as a control problem: ventilators must let air in and out of the patient's lungs according to a prescribed trajectory of airway pressure. Industry-standard controllers, based on the PID method, are neither optimal nor robust. Our data-driven approach learns to control an invasive ventilator by training on a simulator itself trained on data collected from the ventilator. This method outperforms popular reinforcement learning algorithms and even controls the physical ventilator more accurately and robustly than PID. These results underscore how effective data-driven methodologies can be for invasive ventilation and suggest that more general forms of ventilation (e.g., non-invasive, adaptive) may also be amenable.

Provable Regret Bounds for Deep Online Learning and Control

The use of deep neural networks has been highly successful in reinforcement learning and control, although few theoretical guarantees for deep learning exist for these problems. There are two main challenges for deriving performance guarantees: a) control has state information and thus is inherently online and b) deep networks are non-convex predictors for which online learning cannot provide provable guarantees in general. Building on the linearization technique for overparameterized neural networks, we derive provable regret bounds for efficient online learning with deep neural networks. Specifically, we show that over any sequence of convex loss functions, any low-regret algorithm can be adapted to optimize the parameters of a neural network such that it competes with the best net in hindsight. As an application of these results in the online setting, we obtain provable bounds for online episodic control with deep neural network controllers.

Machine Learning for Mechanical Ventilation Control

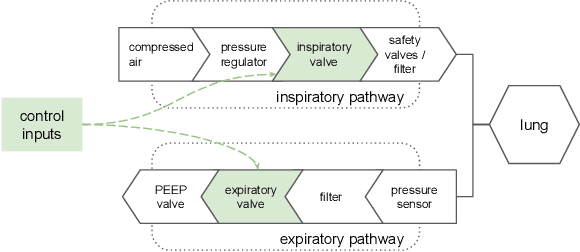
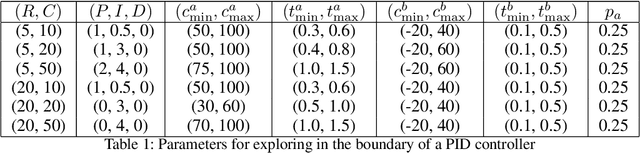
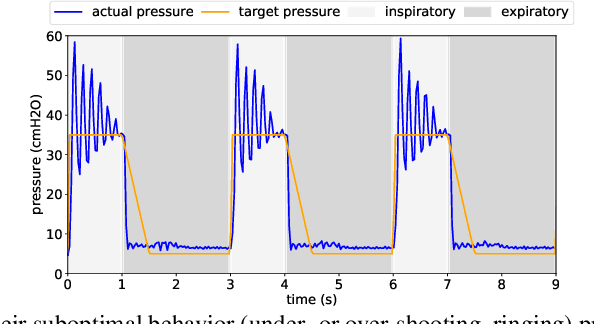
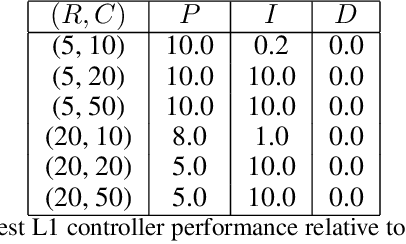
We consider the problem of controlling an invasive mechanical ventilator for pressure-controlled ventilation: a controller must let air in and out of a sedated patient's lungs according to a trajectory of airway pressures specified by a clinician. Hand-tuned PID controllers and similar variants have comprised the industry standard for decades, yet can behave poorly by over- or under-shooting their target or oscillating rapidly. We consider a data-driven machine learning approach: First, we train a simulator based on data we collect from an artificial lung. Then, we train deep neural network controllers on these simulators.We show that our controllers are able to track target pressure waveforms significantly better than PID controllers. We further show that a learned controller generalizes across lungs with varying characteristics much more readily than PID controllers do.

Adaptive Regret for Control of Time-Varying Dynamics

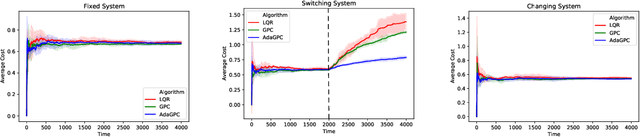
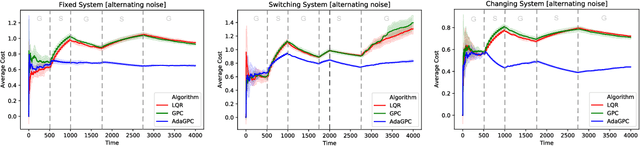
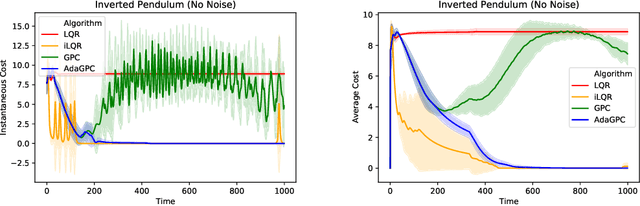
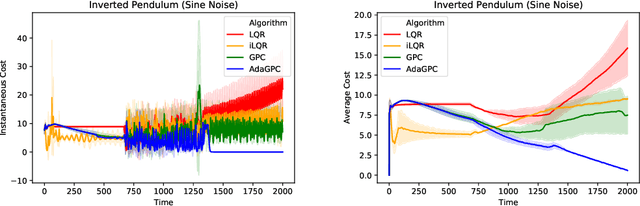
We consider regret minimization for online control with time-varying linear dynamical systems. The metric of performance we study is adaptive policy regret, or regret compared to the best policy on {\it any interval in time}. We give an efficient algorithm that attains first-order adaptive regret guarantees for the setting of online convex optimization with memory. We also show that these first-order bounds are nearly tight. This algorithm is then used to derive a controller with adaptive regret guarantees that provably competes with the best linear dynamical controller on any interval in time. We validate these theoretical findings experimentally on (1) simulations of time-varying linear dynamics and disturbances, and (2) the non-linear inverted pendulum benchmark.

Faster Projection-free Online Learning

In many online learning problems the computational bottleneck for gradient-based methods is the projection operation. For this reason, in many problems the most efficient algorithms are based on the Frank-Wolfe method, which replaces projections by linear optimization. In the general case, however, online projection-free methods require more iterations than projection-based methods: the best known regret bound scales as $T^{3/4}$. Despite significant work on various variants of the Frank-Wolfe method, this bound has remained unchanged for a decade. In this paper we give an efficient projection-free algorithm that guarantees $T^{2/3}$ regret for general online convex optimization with smooth cost functions and one linear optimization computation per iteration. As opposed to previous Frank-Wolfe approaches, our algorithm is derived using the Follow-the-Perturbed-Leader method and is analyzed using an online primal-dual framework.