Adaptive Regret for Control of Time-Varying Dynamics

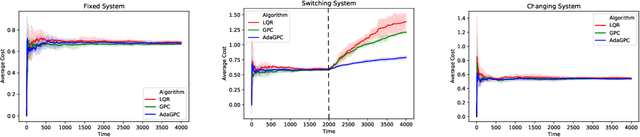
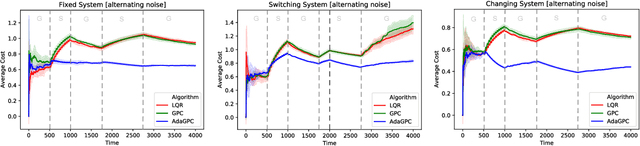
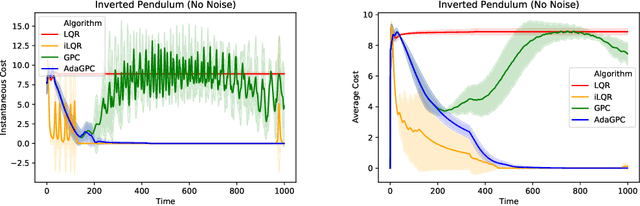
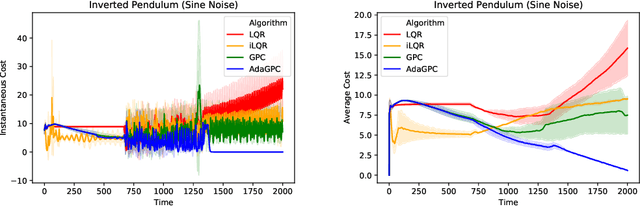
We consider regret minimization for online control with time-varying linear dynamical systems. The metric of performance we study is adaptive policy regret, or regret compared to the best policy on {\it any interval in time}. We give an efficient algorithm that attains first-order adaptive regret guarantees for the setting of online convex optimization with memory. We also show that these first-order bounds are nearly tight. This algorithm is then used to derive a controller with adaptive regret guarantees that provably competes with the best linear dynamical controller on any interval in time. We validate these theoretical findings experimentally on (1) simulations of time-varying linear dynamics and disturbances, and (2) the non-linear inverted pendulum benchmark.