Dongliang Zheng
Delayed Expansion AGT: Kinodynamic Planning with Application to Tractor-Trailer Parking
Jun 16, 2025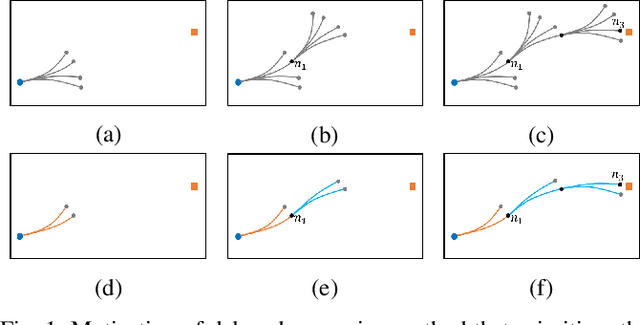
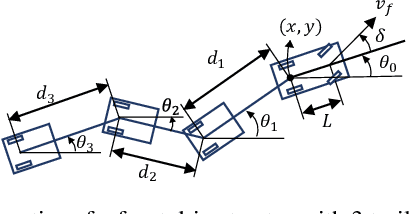
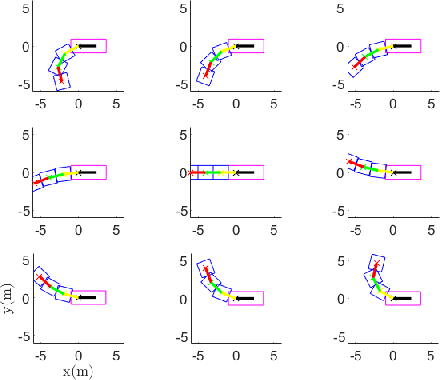
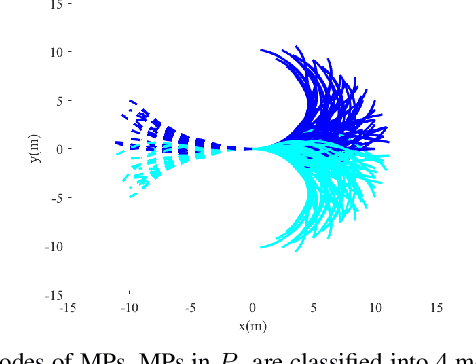
Abstract:Kinodynamic planning of articulated vehicles in cluttered environments faces additional challenges arising from high-dimensional state space and complex system dynamics. Built upon [1],[2], this work proposes the DE-AGT algorithm that grows a tree using pre-computed motion primitives (MPs) and A* heuristics. The first feature of DE-AGT is a delayed expansion of MPs. In particular, the MPs are divided into different modes, which are ranked online. With the MP classification and prioritization, DE-AGT expands the most promising mode of MPs first, which eliminates unnecessary computation and finds solutions faster. To obtain the cost-to-go heuristic for nonholonomic articulated vehicles, we rely on supervised learning and train neural networks for fast and accurate cost-to-go prediction. The learned heuristic is used for online mode ranking and node selection. Another feature of DE-AGT is the improved goal-reaching. Exactly reaching a goal state usually requires a constant connection checking with the goal by solving steering problems -- non-trivial and time-consuming for articulated vehicles. The proposed termination scheme overcomes this challenge by tightly integrating a light-weight trajectory tracking controller with the search process. DE-AGT is implemented for autonomous parking of a general car-like tractor with 3-trailer. Simulation results show an average of 10x acceleration compared to a previous method.
LEA*: An A* Variant Algorithm with Improved Edge Efficiency for Robot Motion Planning
Sep 19, 2023



Abstract:In this work, we introduce a new graph search algorithm, lazy edged based A* (LEA*), for robot motion planning. By using an edge queue and exploiting the idea of lazy search, LEA* is optimally vertex efficient similar to A*, and has improved edge efficiency compared to A*. LEA* is simple and easy to implement with minimum modification to A*, resulting in a very small overhead compared to previous lazy search algorithms. We also explore the effect of inflated heuristics, which results in the weighted LEA* (wLEA*). We show that the edge efficiency of wLEA* becomes close to LazySP and, thus is near-optimal. We test LEA* and wLEA* on 2D planning problems and planning of a 7-DOF manipulator. We perform a thorough comparison with previous algorithms by considering sparse, medium, and cluttered random worlds and small, medium, and large graph sizes. Our results show that LEA* and wLEA* are the fastest algorithms to find the plan compared to previous algorithms.
Kinodynamic FMT* with Dimensionality Reduction Heuristics and Neural Network Controllers
Jun 05, 2023Abstract:This paper proposes a new sampling-based kinodynamic motion planning algorithm, called FMT*PFF, for nonlinear systems. It exploits the novel idea of dimensionality reduction using partial-final-state-free (PFF) optimal controllers.With the proposed dimensionality reduction heuristic, the search space is restricted within a subspace, thus faster convergence is achieved compared to a regular kinodynamic FMT*. The dimensionality reduction heuristic can be viewed as a sampling strategy and asymptotic optimality is preserved when combined with uniform full-state sampling. Another feature of FMT*PFF is the ability to deal with a steering function with inexact steering, which is vital when using learning-based steering functions. Learning-based methods allow us to solve the steering problem for nonlinear systems efficiently. However, learning-based methods often fail to reach the exact goal state. For nonlinear systems, we train a neural network controller using supervised learning to generate the steering commands. We show that FMT*PFF with a learning-based steering function is efficient and generates dynamically feasible motion plans. We compare our algorithm with previous algorithms and show superior performance in various simulations.
IBBT: Informed Batch Belief Trees for Motion Planning Under Uncertainty
Apr 21, 2023



Abstract:In this work, we propose the Informed Batch Belief Trees (IBBT) algorithm for motion planning under motion and sensing uncertainties. The original stochastic motion planning problem is divided into a deterministic motion planning problem and a graph search problem. We solve the deterministic planning problem using sampling-based methods such as PRM or RRG to construct a graph of nominal trajectories. Then, an informed cost-to-go heuristic for the original problem is computed based on the nominal trajectory graph. Finally, we grow a belief tree by searching over the graph using the proposed heuristic. IBBT interleaves between batch state sampling, nominal trajectory graph construction, heuristic computing, and search over the graph to find belief space motion plans. IBBT is an anytime, incremental algorithm. With an increasing number of batches of samples added to the graph, the algorithm finds motion plans that converge to the optimal one. IBBT is efficient by reusing results between sequential iterations. The belief tree searching is an ordered search guided by an informed heuristic. We test IBBT in different planning environments. Our numerical investigation confirms that IBBT finds non-trivial motion plans and is faster compared with previous similar methods.
Indoor simultaneous localization and mapping based on fringe projection profilometry
Apr 23, 2022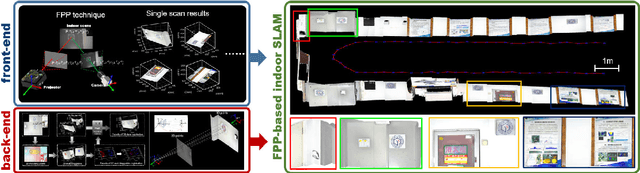
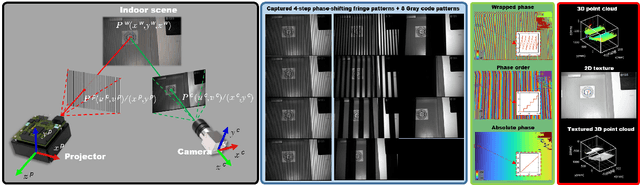
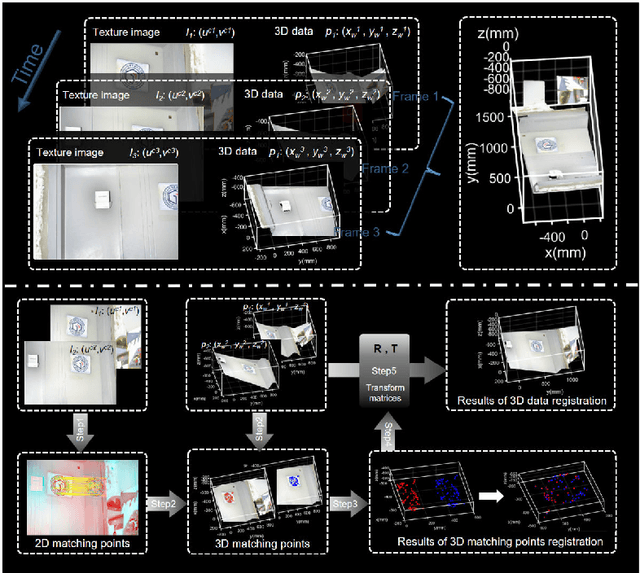
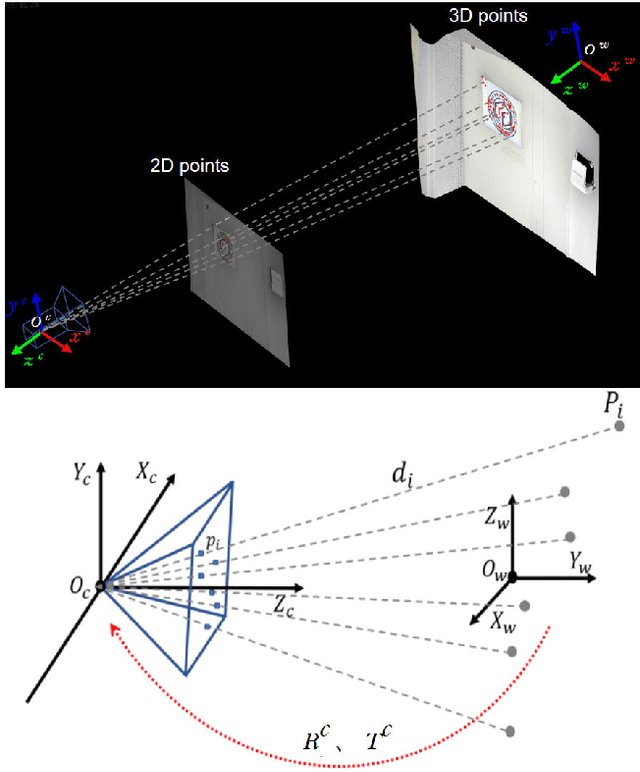
Abstract:Simultaneous Localization and Mapping (SLAM) plays an important role in outdoor and indoor applications ranging from autonomous driving to indoor robotics. Outdoor SLAM has been widely used with the assistance of LiDAR or GPS. For indoor applications, the LiDAR technique does not satisfy the accuracy requirement and the GPS signals will be lost. An accurate and efficient scene sensing technique is required for indoor SLAM. As the most promising 3D sensing technique, the opportunities for indoor SLAM with fringe projection profilometry (FPP) systems are obvious, but methods to date have not fully leveraged the accuracy and speed of sensing that such systems offer. In this paper, we propose a novel FPP-based indoor SLAM method based on the coordinate transformation relationship of FPP, where the 2D-to-3D descriptor-assisted is used for mapping and localization. The correspondences generated by matching descriptors are used for fast and accurate mapping, and the transform estimation between the 2D and 3D descriptors is used to localize the sensor. The provided experimental results demonstrate that the proposed indoor SLAM can achieve the localization and mapping accuracy around one millimeter.
Batch Belief Trees for Motion Planning Under Uncertainty
Oct 01, 2021
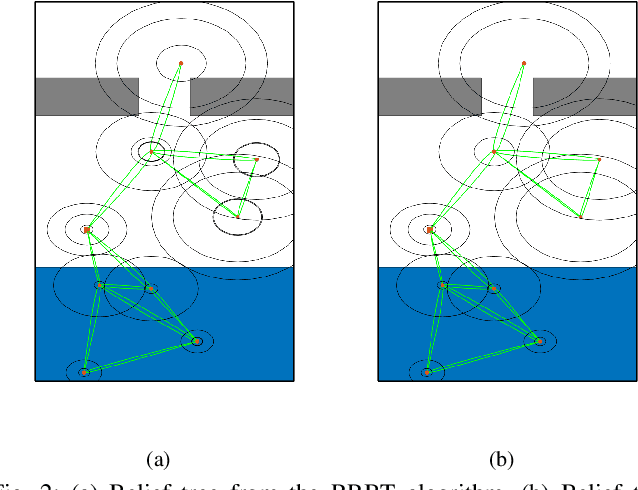
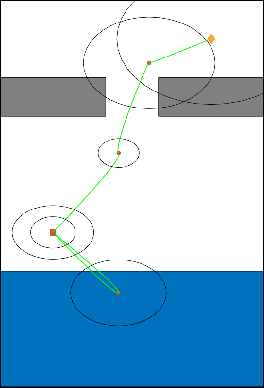
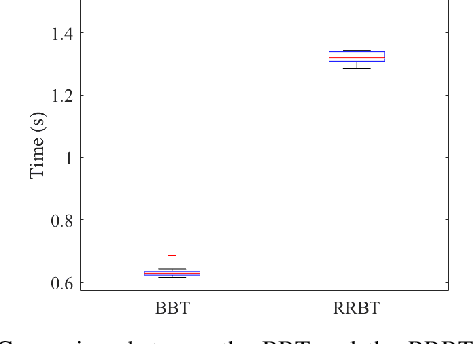
Abstract:In this work, we develop the Batch Belief Trees (BBT) algorithm for motion planning under motion and sensing uncertainties. The algorithm interleaves between batch sampling, building a graph of nominal trajectories in the state space, and searching over the graph to find belief space motion plans. By searching over the graph, BBT finds sophisticated plans that will visit (and revisit) information-rich regions to reduce uncertainty. One of the key benefits of this algorithm is the modified interplay between exploration and exploitation. Instead of an exhaustive search (exploitation) after one exploration step, the proposed algorithm uses batch samples to explore the state space and also does not require exhaustive search before the next iteration of batch sampling, which adds flexibility. The algorithm finds motion plans that converge to the optimal one as more samples are added to the graph. We test BBT in different planning environments. Our numerical investigation confirms that BBT finds non-trivial motion plans and is faster compared with previous similar methods.
Accelerating Kinodynamic RRT* Through Dimensionality Reduction
Jul 02, 2021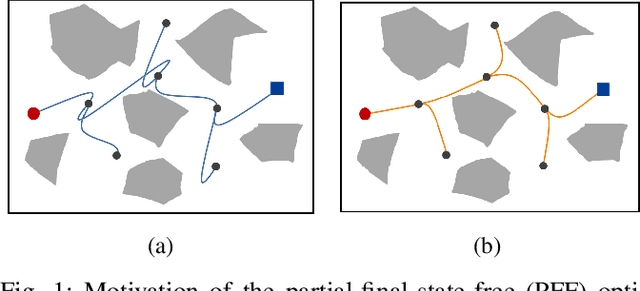
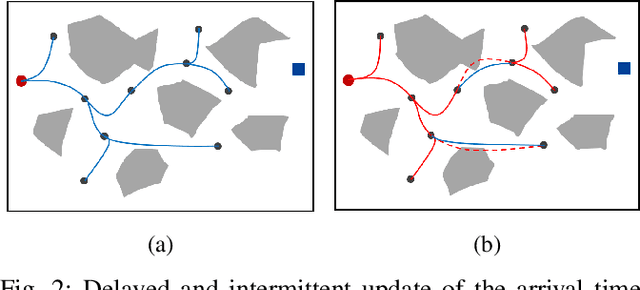


Abstract:Sampling-based motion planning algorithms such as RRT* are well-known for their ability to quickly find an initial solution and then converge to the optimal solution asymptotically. However, the convergence rate can be slow for highdimensional planning problems, particularly for dynamical systems where the sampling space is not just the configuration space but the full state space. In this paper, we introduce the idea of using a partial-final-state-free (PFF) optimal controller in kinodynamic RRT* [1] to reduce the dimensionality of the sampling space. Instead of sampling the full state space, the proposed accelerated kinodynamic RRT*, called Kino-RRT*, only samples part of the state space, while the rest of the states are selected by the PFF optimal controller. We also propose a delayed and intermittent update of the optimal arrival time of all the edges in the RRT* tree to decrease the computation complexity of the algorithm. We tested the proposed algorithm using 4-D and 10-D state-space linear systems and showed that Kino-RRT* converges much faster than the kinodynamic RRT* algorithm.
Belief Space Planning: A Covariance Steering Approach
May 24, 2021

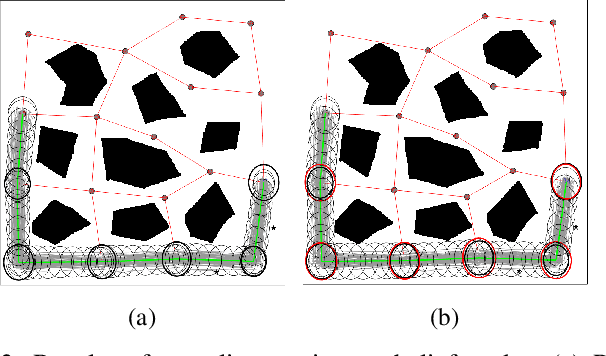

Abstract:A new belief space planning algorithm, called covariance steering Belief RoadMap (CS-BRM), is introduced, which is a multi-query algorithm for motion planning of dynamical systems under simultaneous motion and observation uncertainties. CS-BRM extends the probabilistic roadmap (PRM) approach to belief spaces and is based on the recently developed theory of covariance steering (CS) that enables guaranteed satisfaction of terminal belief constraints in finite-time. The nodes in the CS-BRM are sampled in belief space and represent distributions of the system states. A covariance steering controller steers the system from one BRM node to another, thus acting as an edge controller of the corresponding belief graph that ensures belief constraint satisfaction. After the edge controller is computed, a specific edge cost is assigned to that edge. The CS-BRM algorithm allows the sampling of non-stationary belief nodes, and thus is able to explore the velocity space and find efficient motion plans. The performance of CS-BRM is evaluated and compared to a previous belief space planning method, demonstrating the benefits of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge