The Color Clifford Hardy Signal: Application to Color Edge Detection and Optical Flow

This paper introduces the idea of the color Clifford Hardy signal, which can be used to process color images. As a complex analytic function's high-dimensional analogue, the color Clifford Hardy signal inherits many desirable qualities of analyticity. A crucial tool for getting the color and structural data is the local feature representation of a color image in the color Clifford Hardy signal. By looking at the extended Cauchy-Riemann equations in the high-dimensional space, it is possible to see the connection between the different parts of the color Clifford Hardy signal. Based on the distinctive and important local amplitude and local phase generated by the color Clifford Hardy signal, we propose five methods to identify the edges of color images with relation to a certain color. To prove the superiority of the offered methodologies, numerous comparative studies employing image quality assessment criteria are used. Specifically by using the multi-scale structure of the color Clifford Hardy signal, the proposed approaches are resistant to a variety of noises. In addition, a color optical flow detection method with anti-noise ability is provided as an example of application.

Quaternion Tensor Train Rank Minimization with Sparse Regularization in a Transformed Domain for Quaternion Tensor Completion

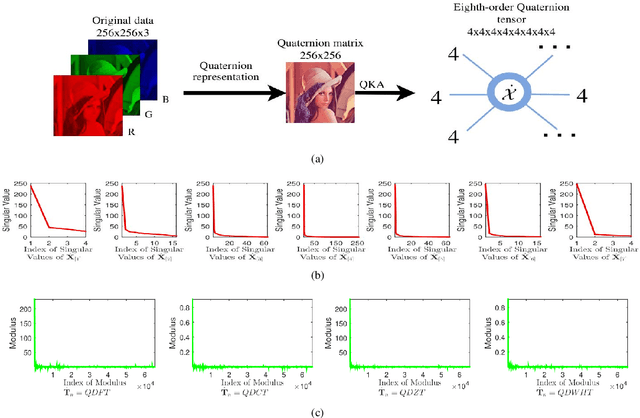
The tensor train rank (TT-rank) has achieved promising results in tensor completion due to its ability to capture the global low-rankness of higher-order (>3) tensors. On the other hand, recently, quaternions have proven to be a very suitable framework for encoding color pixels, and have obtained outstanding performance in various color image processing tasks. In this paper, the quaternion tensor train (QTT) decomposition is presented, and based on that the quaternion TT-rank (QTT-rank) is naturally defined, which are the generalizations of their counterparts in the real number field. In addition, to utilize the local sparse prior of the quaternion tensor, a general and flexible transform framework is defined. Combining both the global low-rank and local sparse priors of the quaternion tensor, we propose a novel quaternion tensor completion model, i.e., QTT-rank minimization with sparse regularization in a transformed domain. Specifically, we use the quaternion weighted nuclear norm (QWNN) of mode-n canonical unfolding quaternion matrices to characterize the global low-QTT-rankness, and the l1-norm of the quaternion tensor in a transformed domain to characterize the local sparse property. Moreover, to enable the QTT-rank minimization to handle color images and better handle color videos, we generalize KA, a tensor augmentation method, to quaternion tensors and define quaternion KA (QKA), which is a helpful pretreatment step for QTT-rank based optimization problems. The numerical experiments on color images and color videos inpainting tasks indicate the advantages of the proposed method over the state-of-the-art ones.

A Robust Lane Detection Associated with Quaternion Hardy Filter

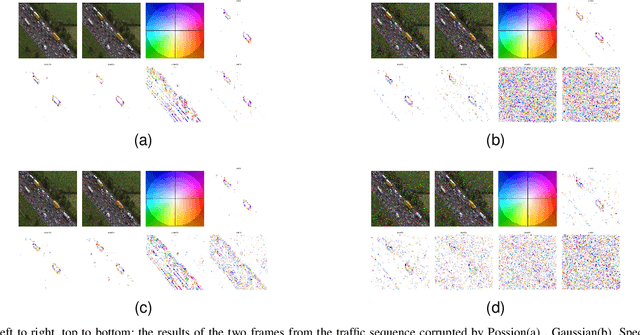
In this article, a robust color-edge feature extraction method based on the Quaternion Hardy filter is proposed. The Quaternion Hardy filter is an emerging edge detection theory. It is along with the Poisson and conjugate Poisson smoothing kernels to handle various types of noise. Combining with the Quaternion Hardy filter, Jin's color gradient operator and Hough transform, the color-edge feature detection algorithm is proposed and applied to the lane marking detection. Experiments are presented to demonstrate the validity of the proposed algorithm. The results are accurate and robust with respect to the complex environment lane markings.