The Color Clifford Hardy Signal: Application to Color Edge Detection and Optical Flow
Paper and Code
Aug 12, 2023
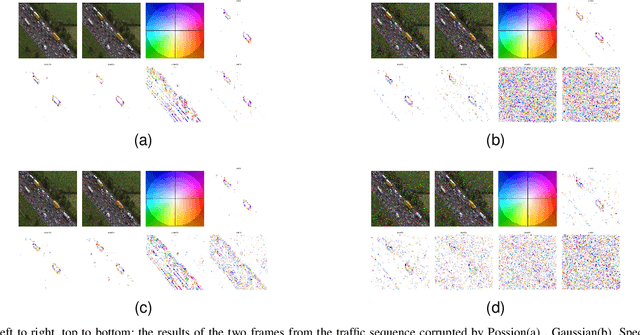


This paper introduces the idea of the color Clifford Hardy signal, which can be used to process color images. As a complex analytic function's high-dimensional analogue, the color Clifford Hardy signal inherits many desirable qualities of analyticity. A crucial tool for getting the color and structural data is the local feature representation of a color image in the color Clifford Hardy signal. By looking at the extended Cauchy-Riemann equations in the high-dimensional space, it is possible to see the connection between the different parts of the color Clifford Hardy signal. Based on the distinctive and important local amplitude and local phase generated by the color Clifford Hardy signal, we propose five methods to identify the edges of color images with relation to a certain color. To prove the superiority of the offered methodologies, numerous comparative studies employing image quality assessment criteria are used. Specifically by using the multi-scale structure of the color Clifford Hardy signal, the proposed approaches are resistant to a variety of noises. In addition, a color optical flow detection method with anti-noise ability is provided as an example of application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge