Non-Negative Reduced Biquaternion Matrix Factorization with Applications in Color Face Recognition

Reduced biquaternion (RB), as a four-dimensional algebra highly suitable for representing color pixels, has recently garnered significant attention from numerous scholars. In this paper, for color image processing problems, we introduce a concept of the non-negative RB matrix and then use the multiplication properties of RB to propose a non-negative RB matrix factorization (NRBMF) model. The NRBMF model is introduced to address the challenge of reasonably establishing a non-negative quaternion matrix factorization model, which is primarily hindered by the multiplication properties of traditional quaternions. Furthermore, this paper transforms the problem of solving the NRBMF model into an RB alternating non-negative least squares (RB-ANNLS) problem. Then, by introducing a method to compute the gradient of the real function with RB matrix variables, we solve the RB-ANNLS optimization problem using the RB projected gradient algorithm and conduct a convergence analysis of the algorithm. Finally, we validate the effectiveness and superiority of the proposed NRBMF model in color face recognition.

$L_{2,1}$-Norm Regularized Quaternion Matrix Completion Using Sparse Representation and Quaternion QR Decomposition

Color image completion is a challenging problem in computer vision, but recent research has shown that quaternion representations of color images perform well in many areas. These representations consider the entire color image and effectively utilize coupling information between the three color channels. Consequently, low-rank quaternion matrix completion (LRQMC) algorithms have gained significant attention. We propose a method based on quaternion Qatar Riyal decomposition (QQR) and quaternion $L_{2,1}$-norm called QLNM-QQR. This new approach reduces computational complexity by avoiding the need to calculate the QSVD of large quaternion matrices. We also present two improvements to the QLNM-QQR method: an enhanced version called IRQLNM-QQR that uses iteratively reweighted quaternion $L_{2,1}$-norm minimization and a method called QLNM-QQR-SR that integrates sparse regularization. Our experiments on natural color images and color medical images show that IRQLNM-QQR outperforms QLNM-QQR and that the proposed QLNM-QQR-SR method is superior to several state-of-the-art methods.

Quaternion tensor ring decomposition and application for color image inpainting

In recent years, tensor networks have emerged as powerful tools for solving large-scale optimization problems. One of the most promising tensor networks is the tensor ring (TR) decomposition, which achieves circular dimensional permutation invariance in the model through the utilization of the trace operation and equitable treatment of the latent cores. On the other hand, more recently, quaternions have gained significant attention and have been widely utilized in color image processing tasks due to their effectiveness in encoding color pixels. Therefore, in this paper, we propose the quaternion tensor ring (QTR) decomposition, which inherits the powerful and generalized representation abilities of the TR decomposition while leveraging the advantages of quaternions for color pixel representation. In addition to providing the definition of QTR decomposition and an algorithm for learning the QTR format, this paper also proposes a low-rank quaternion tensor completion (LRQTC) model and its algorithm for color image inpainting based on the QTR decomposition. Finally, extensive experiments on color image inpainting demonstrate that the proposed QTLRC method is highly competitive.

Quaternion Matrix Completion Using Untrained Quaternion Convolutional Neural Network for Color Image Inpainting

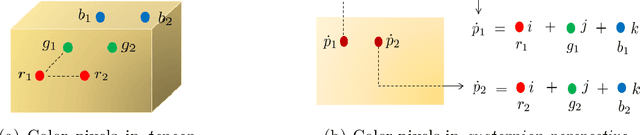
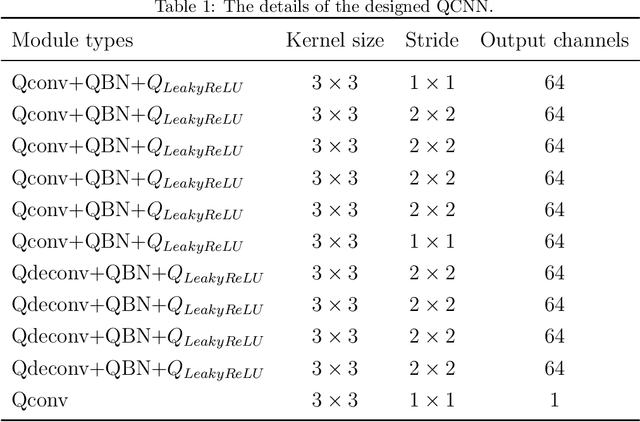
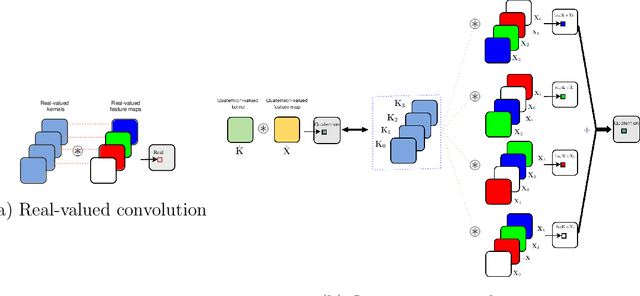
The use of quaternions as a novel tool for color image representation has yielded impressive results in color image processing. By considering the color image as a unified entity rather than separate color space components, quaternions can effectively exploit the strong correlation among the RGB channels, leading to enhanced performance. Especially, color image inpainting tasks are highly beneficial from the application of quaternion matrix completion techniques, in recent years. However, existing quaternion matrix completion methods suffer from two major drawbacks. First, it can be difficult to choose a regularizer that captures the common characteristics of natural images, and sometimes the regularizer that is chosen based on empirical evidence may not be the optimal or efficient option. Second, the optimization process of quaternion matrix completion models is quite challenging because of the non-commutativity of quaternion multiplication. To address the two drawbacks of the existing quaternion matrix completion approaches mentioned above, this paper tends to use an untrained quaternion convolutional neural network (QCNN) to directly generate the completed quaternion matrix. This approach replaces the explicit regularization term in the quaternion matrix completion model with an implicit prior that is learned by the QCNN. Extensive quantitative and qualitative evaluations demonstrate the superiority of the proposed method for color image inpainting compared with some existing quaternion-based and tensor-based methods.

Quaternion Tensor Completion with Sparseness for Color Video Recovery

A novel low-rank completion algorithm based on the quaternion tensor is proposed in this paper. This approach uses the TQt-rank of quaternion tensor to maintain the structure of RGB channels throughout the entire process. In more detail, the pixels in each frame are encoded on three imaginary parts of a quaternion as an element in a quaternion matrix. Each quaternion matrix is then stacked into a quaternion tensor. A logarithmic function and truncated nuclear norm are employed to characterize the rank of the quaternion tensor in order to promote the low rankness of the tensor. Moreover, by introducing a newly defined quaternion tensor discrete cosine transform-based (QTDCT) regularization to the low-rank approximation framework, the optimized recovery results can be obtained in the local details of color videos. In particular, the sparsity of the quaternion tensor is reasonably characterized by l1 norm in the QDCT domain. This strategy is optimized via the two-step alternating direction method of multipliers (ADMM) framework. Numerical experimental results for recovering color videos show the obvious advantage of the proposed method over other potential competing approaches.

Low Rank Quaternion Matrix Completion Based on Quaternion QR Decomposition and Sparse Regularizer

Matrix completion is one of the most challenging problems in computer vision. Recently, quaternion representations of color images have achieved competitive performance in many fields. Because it treats the color image as a whole, the coupling information between the three channels of the color image is better utilized. Due to this, low-rank quaternion matrix completion (LRQMC) algorithms have gained considerable attention from researchers. In contrast to the traditional quaternion matrix completion algorithms based on quaternion singular value decomposition (QSVD), we propose a novel method based on quaternion Qatar Riyal decomposition (QQR). In the first part of the paper, a novel method for calculating an approximate QSVD based on iterative QQR is proposed (CQSVD-QQR), whose computational complexity is lower than that of QSVD. The largest $r \ (r>0)$ singular values of a given quaternion matrix can be computed by using CQSVD-QQR. Then, we propose a new quaternion matrix completion method based on CQSVD-QQR which combines low-rank and sparse priors of color images. Experimental results on color images and color medical images demonstrate that our model outperforms those state-of-the-art methods.

Quaternion Tensor Train Rank Minimization with Sparse Regularization in a Transformed Domain for Quaternion Tensor Completion

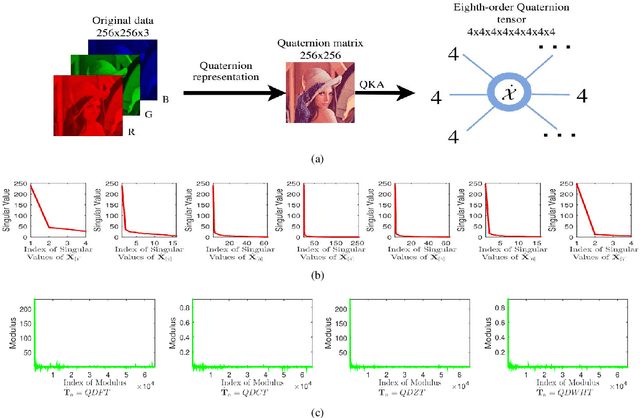
The tensor train rank (TT-rank) has achieved promising results in tensor completion due to its ability to capture the global low-rankness of higher-order (>3) tensors. On the other hand, recently, quaternions have proven to be a very suitable framework for encoding color pixels, and have obtained outstanding performance in various color image processing tasks. In this paper, the quaternion tensor train (QTT) decomposition is presented, and based on that the quaternion TT-rank (QTT-rank) is naturally defined, which are the generalizations of their counterparts in the real number field. In addition, to utilize the local sparse prior of the quaternion tensor, a general and flexible transform framework is defined. Combining both the global low-rank and local sparse priors of the quaternion tensor, we propose a novel quaternion tensor completion model, i.e., QTT-rank minimization with sparse regularization in a transformed domain. Specifically, we use the quaternion weighted nuclear norm (QWNN) of mode-n canonical unfolding quaternion matrices to characterize the global low-QTT-rankness, and the l1-norm of the quaternion tensor in a transformed domain to characterize the local sparse property. Moreover, to enable the QTT-rank minimization to handle color images and better handle color videos, we generalize KA, a tensor augmentation method, to quaternion tensors and define quaternion KA (QKA), which is a helpful pretreatment step for QTT-rank based optimization problems. The numerical experiments on color images and color videos inpainting tasks indicate the advantages of the proposed method over the state-of-the-art ones.

Quaternion-based dynamic mode decomposition for background modeling in color videos

Scene Background Initialization (SBI) is one of the challenging problems in computer vision. Dynamic mode decomposition (DMD) is a recently proposed method to robustly decompose a video sequence into the background model and the corresponding foreground part. However, this method needs to convert the color image into the grayscale image for processing, which leads to the neglect of the coupling information between the three channels of the color image. In this study, we propose a quaternion-based DMD (Q-DMD), which extends the DMD by quaternion matrix analysis, so as to completely preserve the inherent color structure of the color image and the color video. We exploit the standard eigenvalues of the quaternion matrix to compute its spectral decomposition and calculate the corresponding Q-DMD modes and eigenvalues. The results on the publicly available benchmark datasets prove that our Q-DMD outperforms the exact DMD method, and experiment results also demonstrate that the performance of our approach is comparable to that of the state-of-the-art ones.

Low Rank Quaternion Matrix Recovery via Logarithmic Approximation

In color image processing, image completion aims to restore missing entries from the incomplete observation image. Recently, great progress has been made in achieving completion by approximately solving the rank minimization problem. In this paper, we utilize a novel quaternion matrix logarithmic norm to approximate rank under the quaternion matrix framework. From one side, unlike the traditional matrix completion method that handles RGB channels separately, the quaternion-based method is able to avoid destroying the structure of images via putting the color image in a pure quaternion matrix. From the other side, the logarithmic norm induces a more accurate rank surrogate. Based on the logarithmic norm, we take advantage of not only truncated technique but also factorization strategy to achieve image restoration. Both strategies are optimized based on the alternating minimization framework. The experimental results demonstrate that the use of logarithmic surrogates in the quaternion domain is more superior in solving the problem of color images completion.

Weighted Truncated Nuclear Norm Regularization for Low-Rank Quaternion Matrix Completion

In recent years, quaternion matrix completion (QMC) based on low-rank regularization has been gradually used in image de-noising and de-blurring.Unlike low-rank matrix completion (LRMC) which handles RGB images by recovering each color channel separately, the QMC models utilize the connection of three channels by processing them as a whole. Most of the existing quaternion-based methods formulate low-rank QMC (LRQMC) as a quaternion nuclear norm (a convex relaxation of the rank) minimization problem.The main limitation of these approaches is that the singular values being minimized simultaneously so that the low-rank property could not be approximated well and efficiently. To achieve a more accurate low-rank approximation, the matrix-based truncated nuclear norm has been proposed and also been proved to have the superiority. In this paper, we introduce a quaternion truncated nuclear norm (QTNN) for LRQMC and utilize the alternating direction method of multipliers (ADMM) to get the optimization.We further propose weights to the residual error quaternion matrix during the update process for accelerating the convergence of the QTNN method with admissible performance. The weighted method utilizes a concise gradient descent strategy which has a theoretical guarantee in optimization. The effectiveness of our method is illustrated by experiments on real visual datasets.