Quaternion Tensor Train Rank Minimization with Sparse Regularization in a Transformed Domain for Quaternion Tensor Completion
Paper and Code
Sep 07, 2022
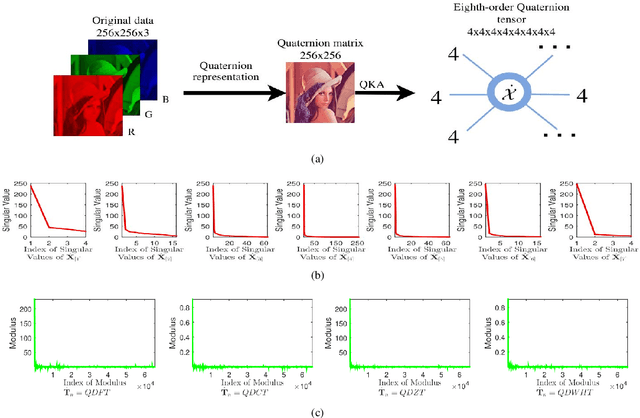

The tensor train rank (TT-rank) has achieved promising results in tensor completion due to its ability to capture the global low-rankness of higher-order (>3) tensors. On the other hand, recently, quaternions have proven to be a very suitable framework for encoding color pixels, and have obtained outstanding performance in various color image processing tasks. In this paper, the quaternion tensor train (QTT) decomposition is presented, and based on that the quaternion TT-rank (QTT-rank) is naturally defined, which are the generalizations of their counterparts in the real number field. In addition, to utilize the local sparse prior of the quaternion tensor, a general and flexible transform framework is defined. Combining both the global low-rank and local sparse priors of the quaternion tensor, we propose a novel quaternion tensor completion model, i.e., QTT-rank minimization with sparse regularization in a transformed domain. Specifically, we use the quaternion weighted nuclear norm (QWNN) of mode-n canonical unfolding quaternion matrices to characterize the global low-QTT-rankness, and the l1-norm of the quaternion tensor in a transformed domain to characterize the local sparse property. Moreover, to enable the QTT-rank minimization to handle color images and better handle color videos, we generalize KA, a tensor augmentation method, to quaternion tensors and define quaternion KA (QKA), which is a helpful pretreatment step for QTT-rank based optimization problems. The numerical experiments on color images and color videos inpainting tasks indicate the advantages of the proposed method over the state-of-the-art ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge