$L_{2,1}$-Norm Regularized Quaternion Matrix Completion Using Sparse Representation and Quaternion QR Decomposition

Color image completion is a challenging problem in computer vision, but recent research has shown that quaternion representations of color images perform well in many areas. These representations consider the entire color image and effectively utilize coupling information between the three color channels. Consequently, low-rank quaternion matrix completion (LRQMC) algorithms have gained significant attention. We propose a method based on quaternion Qatar Riyal decomposition (QQR) and quaternion $L_{2,1}$-norm called QLNM-QQR. This new approach reduces computational complexity by avoiding the need to calculate the QSVD of large quaternion matrices. We also present two improvements to the QLNM-QQR method: an enhanced version called IRQLNM-QQR that uses iteratively reweighted quaternion $L_{2,1}$-norm minimization and a method called QLNM-QQR-SR that integrates sparse regularization. Our experiments on natural color images and color medical images show that IRQLNM-QQR outperforms QLNM-QQR and that the proposed QLNM-QQR-SR method is superior to several state-of-the-art methods.

Quaternion Matrix Completion Using Untrained Quaternion Convolutional Neural Network for Color Image Inpainting

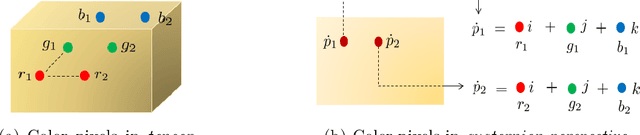
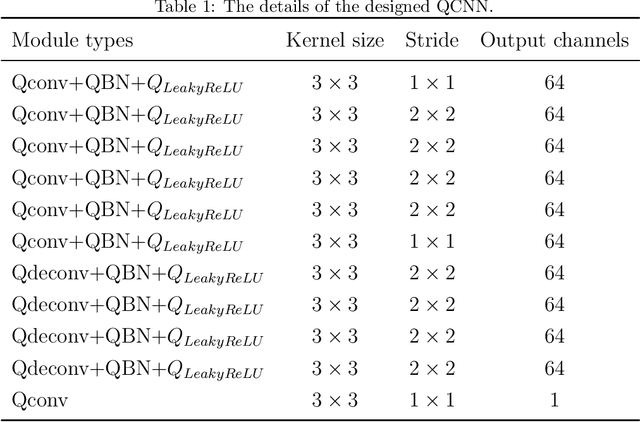
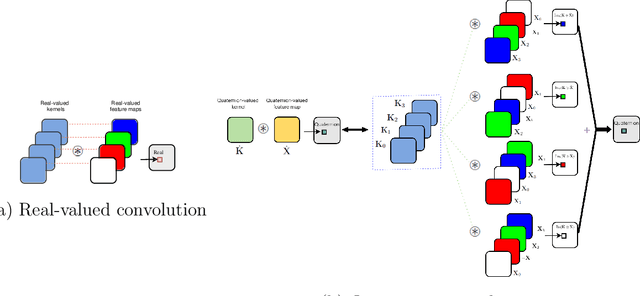
The use of quaternions as a novel tool for color image representation has yielded impressive results in color image processing. By considering the color image as a unified entity rather than separate color space components, quaternions can effectively exploit the strong correlation among the RGB channels, leading to enhanced performance. Especially, color image inpainting tasks are highly beneficial from the application of quaternion matrix completion techniques, in recent years. However, existing quaternion matrix completion methods suffer from two major drawbacks. First, it can be difficult to choose a regularizer that captures the common characteristics of natural images, and sometimes the regularizer that is chosen based on empirical evidence may not be the optimal or efficient option. Second, the optimization process of quaternion matrix completion models is quite challenging because of the non-commutativity of quaternion multiplication. To address the two drawbacks of the existing quaternion matrix completion approaches mentioned above, this paper tends to use an untrained quaternion convolutional neural network (QCNN) to directly generate the completed quaternion matrix. This approach replaces the explicit regularization term in the quaternion matrix completion model with an implicit prior that is learned by the QCNN. Extensive quantitative and qualitative evaluations demonstrate the superiority of the proposed method for color image inpainting compared with some existing quaternion-based and tensor-based methods.

Low Rank Quaternion Matrix Completion Based on Quaternion QR Decomposition and Sparse Regularizer

Matrix completion is one of the most challenging problems in computer vision. Recently, quaternion representations of color images have achieved competitive performance in many fields. Because it treats the color image as a whole, the coupling information between the three channels of the color image is better utilized. Due to this, low-rank quaternion matrix completion (LRQMC) algorithms have gained considerable attention from researchers. In contrast to the traditional quaternion matrix completion algorithms based on quaternion singular value decomposition (QSVD), we propose a novel method based on quaternion Qatar Riyal decomposition (QQR). In the first part of the paper, a novel method for calculating an approximate QSVD based on iterative QQR is proposed (CQSVD-QQR), whose computational complexity is lower than that of QSVD. The largest $r \ (r>0)$ singular values of a given quaternion matrix can be computed by using CQSVD-QQR. Then, we propose a new quaternion matrix completion method based on CQSVD-QQR which combines low-rank and sparse priors of color images. Experimental results on color images and color medical images demonstrate that our model outperforms those state-of-the-art methods.

Quaternion-based dynamic mode decomposition for background modeling in color videos

Scene Background Initialization (SBI) is one of the challenging problems in computer vision. Dynamic mode decomposition (DMD) is a recently proposed method to robustly decompose a video sequence into the background model and the corresponding foreground part. However, this method needs to convert the color image into the grayscale image for processing, which leads to the neglect of the coupling information between the three channels of the color image. In this study, we propose a quaternion-based DMD (Q-DMD), which extends the DMD by quaternion matrix analysis, so as to completely preserve the inherent color structure of the color image and the color video. We exploit the standard eigenvalues of the quaternion matrix to compute its spectral decomposition and calculate the corresponding Q-DMD modes and eigenvalues. The results on the publicly available benchmark datasets prove that our Q-DMD outperforms the exact DMD method, and experiment results also demonstrate that the performance of our approach is comparable to that of the state-of-the-art ones.