Verifying Relational Explanations: A Probabilistic Approach

Explanations on relational data are hard to verify since the explanation structures are more complex (e.g. graphs). To verify interpretable explanations (e.g. explanations of predictions made in images, text, etc.), typically human subjects are used since it does not necessarily require a lot of expertise. However, to verify the quality of a relational explanation requires expertise and is hard to scale-up. GNNExplainer is arguably one of the most popular explanation methods for Graph Neural Networks. In this paper, we develop an approach where we assess the uncertainty in explanations generated by GNNExplainer. Specifically, we ask the explainer to generate explanations for several counterfactual examples. We generate these examples as symmetric approximations of the relational structure in the original data. From these explanations, we learn a factor graph model to quantify uncertainty in an explanation. Our results on several datasets show that our approach can help verify explanations from GNNExplainer by reliably estimating the uncertainty of a relation specified in the explanation.

On the verification of Embeddings using Hybrid Markov Logic

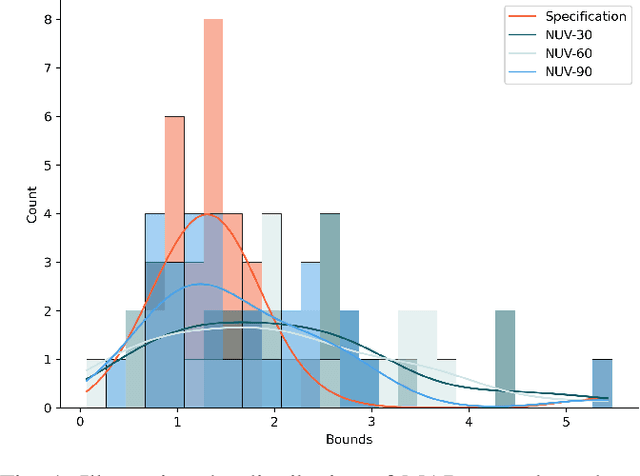
The standard approach to verify representations learned by Deep Neural Networks is to use them in specific tasks such as classification or regression, and measure their performance based on accuracy in such tasks. However, in many cases, we would want to verify more complex properties of a learned representation. To do this, we propose a framework based on a probabilistic first-order language, namely, Hybrid Markov Logic Networks (HMLNs) where we specify properties over embeddings mixed with symbolic domain knowledge. We present an approach to learn parameters for the properties within this framework. Further, we develop a verification method to test embeddings in this framework by encoding this task as a Mixed Integer Linear Program for which we can leverage existing state-of-the-art solvers. We illustrate verification in Graph Neural Networks, Deep Knowledge Tracing and Intelligent Tutoring Systems to demonstrate the generality of our approach.

Scalable and Equitable Math Problem Solving Strategy Prediction in Big Educational Data

Understanding a student's problem-solving strategy can have a significant impact on effective math learning using Intelligent Tutoring Systems (ITSs) and Adaptive Instructional Systems (AISs). For instance, the ITS/AIS can better personalize itself to correct specific misconceptions that are indicated by incorrect strategies, specific problems can be designed to improve strategies and frustration can be minimized by adapting to a student's natural way of thinking rather than trying to fit a standard strategy for all. While it may be possible for human experts to identify strategies manually in classroom settings with sufficient student interaction, it is not possible to scale this up to big data. Therefore, we leverage advances in Machine Learning and AI methods to perform scalable strategy prediction that is also fair to students at all skill levels. Specifically, we develop an embedding called MVec where we learn a representation based on the mastery of students. We then cluster these embeddings with a non-parametric clustering method where we progressively learn clusters such that we group together instances that have approximately symmetrical strategies. The strategy prediction model is trained on instances sampled from these clusters. This ensures that we train the model over diverse strategies and also that strategies from a particular group do not bias the DNN model, thus allowing it to optimize its parameters over all groups. Using real world large-scale student interaction datasets from MATHia, we implement our approach using transformers and Node2Vec for learning the mastery embeddings and LSTMs for predicting strategies. We show that our approach can scale up to achieve high accuracy by training on a small sample of a large dataset and also has predictive equality, i.e., it can predict strategies equally well for learners at diverse skill levels.

CIDMP: Completely Interpretable Detection of Malaria Parasite in Red Blood Cells using Lower-dimensional Feature Space

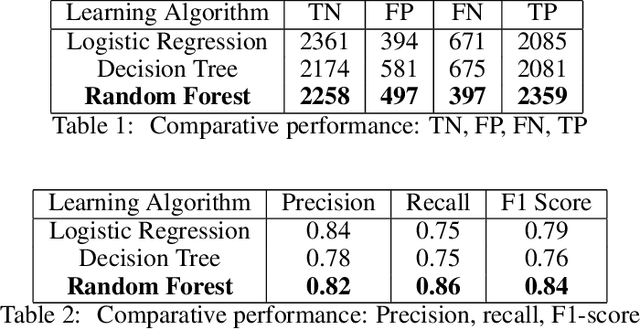
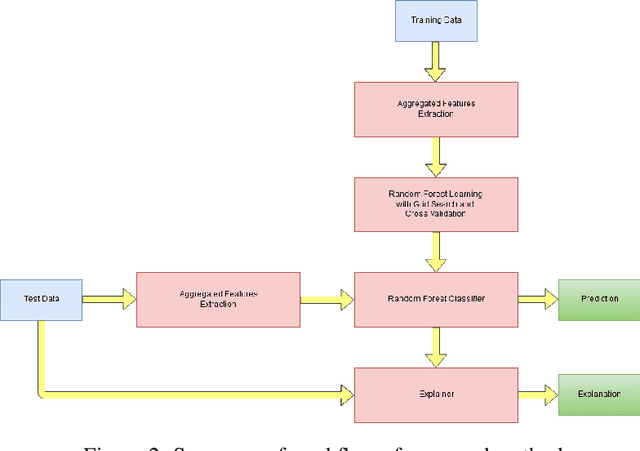
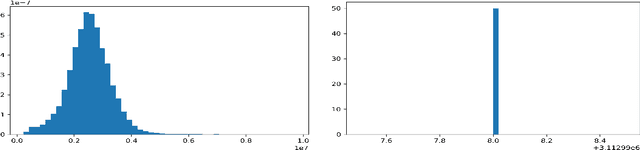
Predicting if red blood cells (RBC) are infected with the malaria parasite is an important problem in Pathology. Recently, supervised machine learning approaches have been used for this problem, and they have had reasonable success. In particular, state-of-the-art methods such as Convolutional Neural Networks automatically extract increasingly complex feature hierarchies from the image pixels. While such generalized automatic feature extraction methods have significantly reduced the burden of feature engineering in many domains, for niche tasks such as the one we consider in this paper, they result in two major problems. First, they use a very large number of features (that may or may not be relevant) and therefore training such models is computationally expensive. Further, more importantly, the large feature-space makes it very hard to interpret which features are truly important for predictions. Thus, a criticism of such methods is that learning algorithms pose opaque black boxes to its users, in this case, medical experts. The recommendation of such algorithms can be understood easily, but the reason for their recommendation is not clear. This is the problem of non-interpretability of the model, and the best-performing algorithms are usually the least interpretable. To address these issues, in this paper, we propose an approach to extract a very small number of aggregated features that are easy to interpret and compute, and empirically show that we obtain high prediction accuracy even with a significantly reduced feature-space.

Dynamic Blocking and Collapsing for Gibbs Sampling

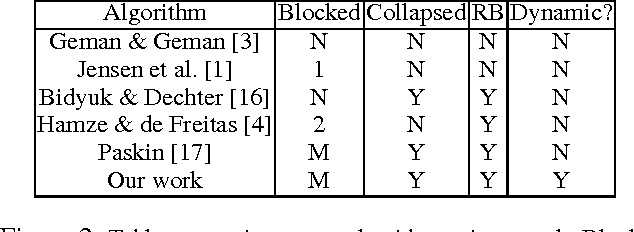
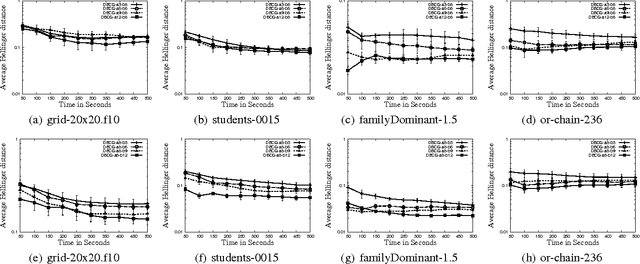
In this paper, we investigate combining blocking and collapsing -- two widely used strategies for improving the accuracy of Gibbs sampling -- in the context of probabilistic graphical models (PGMs). We show that combining them is not straight-forward because collapsing (or eliminating variables) introduces new dependencies in the PGM and in computation-limited settings, this may adversely affect blocking. We therefore propose a principled approach for tackling this problem. Specifically, we develop two scoring functions, one each for blocking and collapsing, and formulate the problem of partitioning the variables in the PGM into blocked and collapsed subsets as simultaneously maximizing both scoring functions (i.e., a multi-objective optimization problem). We propose a dynamic, greedy algorithm for approximately solving this intractable optimization problem. Our dynamic algorithm periodically updates the partitioning into blocked and collapsed variables by leveraging correlation statistics gathered from the generated samples and enables rapid mixing by blocking together and collapsing highly correlated variables. We demonstrate experimentally the clear benefit of our dynamic approach: as more samples are drawn, our dynamic approach significantly outperforms static graph-based approaches by an order of magnitude in terms of accuracy.