Dynamic Blocking and Collapsing for Gibbs Sampling
Paper and Code
Sep 26, 2013
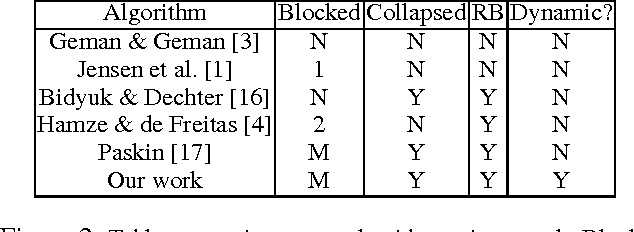

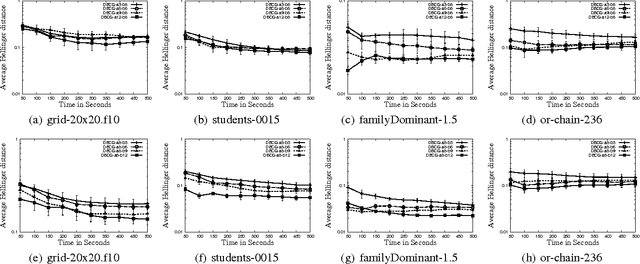
In this paper, we investigate combining blocking and collapsing -- two widely used strategies for improving the accuracy of Gibbs sampling -- in the context of probabilistic graphical models (PGMs). We show that combining them is not straight-forward because collapsing (or eliminating variables) introduces new dependencies in the PGM and in computation-limited settings, this may adversely affect blocking. We therefore propose a principled approach for tackling this problem. Specifically, we develop two scoring functions, one each for blocking and collapsing, and formulate the problem of partitioning the variables in the PGM into blocked and collapsed subsets as simultaneously maximizing both scoring functions (i.e., a multi-objective optimization problem). We propose a dynamic, greedy algorithm for approximately solving this intractable optimization problem. Our dynamic algorithm periodically updates the partitioning into blocked and collapsed variables by leveraging correlation statistics gathered from the generated samples and enables rapid mixing by blocking together and collapsing highly correlated variables. We demonstrate experimentally the clear benefit of our dynamic approach: as more samples are drawn, our dynamic approach significantly outperforms static graph-based approaches by an order of magnitude in terms of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge